【题目】二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+b2﹣4ac与反比例函数y= ![]() 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( ) 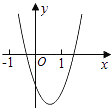
A.
B.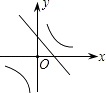
C.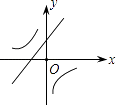
D.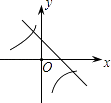
参考答案:
【答案】D
【解析】解:由抛物线的图象可知,横坐标为1的点,即(1,a+b+c)在第四象限,因此a+b+c<0; ∴双曲线 ![]() 的图象在第二、四象限;
的图象在第二、四象限;
由于抛物线开口向上,所以a>0;
对称轴x= ![]() >0,所以b<0;
>0,所以b<0;
抛物线与x轴有两个交点,故b2﹣4ac>0;
∴直线y=bx+b2﹣4ac经过第一、二、四象限.
故选:D.
【考点精析】本题主要考查了一次函数的图象和性质和反比例函数的图象的相关知识点,需要掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘海轮位于灯塔P的东北方向,距离灯塔40
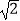 海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为( )海里.
海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处,则海轮行驶的路程AB为( )海里. 
A.40+40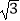
B.80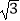
C.40+20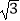
D.80 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,D,E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
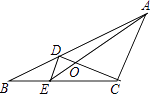
A.1:3
B.1:4
C.1:5
D.1:25 -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC和△A′B′C′中,①AB=A′B′,②BC=B′C′,③AC=A′C′,④∠A=∠A′,⑤∠B=∠B′,⑥∠C=∠C′,则下列各组条件中使△ABC和△A′B′C′全等的是( )
A. ④⑤⑥ B. ①②⑥ C. ①③⑤ D. ②⑤⑥
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠ABC=70°,以B为圆心,任意长为半径画弧交AB,BC于点E,F,再分别以点E,F为圆心、以大于
 EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.
EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.
A. 65 B. 75 C. 80 D. 85
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角形纸片的两直角边长分别为4,8,现将△ABC如图那样折叠,使点A与点B重合,折痕为DE,则tan∠CBE的值是 .
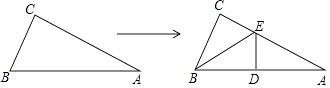
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ACB中,∠ACB=90°,∠ABC的平分线BE和∠BAC的外角平分线AD相交于点P,分别交AC和BC的延长线于E,D.过P作PF⊥AD交AC的延长线于点H,交BC的延长线于点F,连接AF交DH于点G.则下列结论:①∠APB=45°;②PF=PA;③BD﹣AH=AB;④DG=AP+GH.其中正确的是( )

A. ①②③ B. ①②④ C. ②③④ D. ①②③④
相关试题

