【题目】己知数轴上![]() 三点对应的数分别为
三点对应的数分别为![]() 、3、5,点
、3、5,点![]() 为数轴上任意一点,其对应的数为
为数轴上任意一点,其对应的数为![]() .点
.点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() .
.
(1)若![]() ,则
,则![]() ;
;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若点![]() 从点
从点![]() 出发,以每秒3个单位的速度向右运动,点
出发,以每秒3个单位的速度向右运动,点![]() 以每秒1个单位的速度向左运动,点
以每秒1个单位的速度向左运动,点![]() 以每秒2个单位的速度向右运动,三点同时出发.设运动时间为
以每秒2个单位的速度向右运动,三点同时出发.设运动时间为![]() 秒,试判断:
秒,试判断:![]() 的值是否会随着
的值是否会随着![]() 的变化而变化?请说明理由.
的变化而变化?请说明理由.

参考答案:
【答案】(1)1;(2)![]() 的值为
的值为![]() 或5;(3)不会,理由见解析
或5;(3)不会,理由见解析
【解析】
(1)根据题意,若![]() ,则是表明P在A、B两点之间的中点位置,据此得出答案即可;
,则是表明P在A、B两点之间的中点位置,据此得出答案即可;
(2)分P点在A左侧以及P点在B右侧两种情况讨论即可.
(3)根据题意先将BP的距离的代数式列出来为![]() ,AP的距离的代数式为
,AP的距离的代数式为![]() ,然后代入
,然后代入![]() 计算观察其结果是否与t有关即可.
计算观察其结果是否与t有关即可.
(1)∵![]() ,∴P在A、B两点之间的中点位置,
,∴P在A、B两点之间的中点位置,
∴P到B的距离为![]() ,∴P表示的数为
,∴P表示的数为![]() .
.
所以答案为1;
(2)①当P点在A左侧时:![]() ,
,
∴![]() ;
;
②当P点在B右侧时:![]() ,
,
∴![]() ;
;
综上所述,![]() 的值为
的值为![]() 或5;
或5;
(3)不会,理由如下:
由题意得:BP=![]() ,AP=
,AP=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() 的值不会随着
的值不会随着![]() 的变化而变化.
的变化而变化.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是假命题的是( )
A. 过
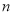 边形一个顶点的所有对角线,将这个多边形分成
边形一个顶点的所有对角线,将这个多边形分成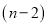 个三角形
个三角形B. 三角形中,到三个顶点距离相等的点是三条边垂直平分线的交点
C. 三角形的中线将三角形分成面积相等的两部分
D. 一组对边平行另一组对边相等的四边形是平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
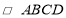 中,
中,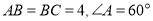 ,连接
,连接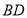 ,将
,将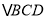 绕点
绕点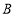 旋转,当
旋转,当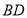 (即
(即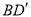 )与
)与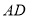 交于一点
交于一点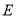 ,
,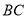 (即
(即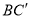 )与
)与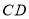 交于一点
交于一点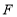 时,给出以下结论:①
时,给出以下结论:①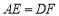 ;②
;②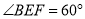 ;③
;③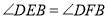 ;④
;④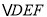 的周长的最小值是
的周长的最小值是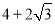 .其中正确的是( )
.其中正确的是( )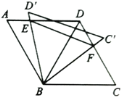
A. ①②③B. ①②④C. ②③④D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四边形
 中,
中, ,
, 分别是
分别是 的中点,
的中点, ,则
,则 的长是___________.
的长是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们环保意识的增强,越来越多的人选择低碳出行,各种品牌的山地自行车相继投放市场.顺风车行五月份
 型车的销售总利润为
型车的销售总利润为 元,
元, 型车的销售总利润为
型车的销售总利润为 元.且
元.且 型车的销售数量是
型车的销售数量是 型车的
型车的 倍,已知销售
倍,已知销售 型车比
型车比 型车每辆可多获利
型车每辆可多获利 元.
元.(1)求每辆
 型车和
型车和 型车的销售利润;
型车的销售利润;(2)若该车行计划一次购进
 两种型号的自行车共
两种型号的自行车共 台且全部售出,其中
台且全部售出,其中 型车的进货数量不超过
型车的进货数量不超过 型车的
型车的 倍,则该车行购进
倍,则该车行购进 型车、
型车、 型车各多少辆,才能使销售总利润最大?最大销售总利润是多少?
型车各多少辆,才能使销售总利润最大?最大销售总利润是多少? -
科目: 来源: 题型:
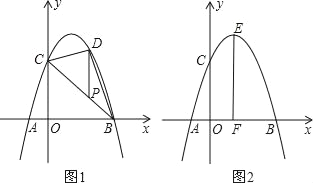
查看答案和解析>>【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
相关试题

