【题目】小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果小明想要每月获得的利润不低于2000元,那么小明每月的成本最少需要多少元?(成本=进价×销售量)
参考答案:
【答案】(1![]() (20≤x≤32);(2)当销售单价定为32元时,每月可获得最大利润,最大利润是2160元;(3)3600.
(20≤x≤32);(2)当销售单价定为32元时,每月可获得最大利润,最大利润是2160元;(3)3600.
【解析】试题分析:(1)由题意得,每月销售量与销售单价之间的关系可近似看作一次函数,利润=(定价﹣进价)×销售量,从而列出关系式;
(2)首先确定二次函数的对称轴,然后根据其增减性确定最大利润即可;
(3)根据抛物线的性质和图象,求出每月的成本.
试题解析:(1)由题意,得:w=(x﹣20)y=(x﹣20)(﹣10x+500)=![]() ,即
,即![]() (20≤x≤32);
(20≤x≤32);
(2)对于函数![]() 的图象的对称轴是直线x=
的图象的对称轴是直线x=![]() =35.
=35.
又∵a=﹣10<0,抛物线开口向下.∴当20≤x≤32时,W随着X的增大而增大,∴当x=32时,W=2160
答:当销售单价定为32元时,每月可获得最大利润,最大利润是2160元.
(3)取W=2000得,![]()
解这个方程得: ![]() =30,
=30, ![]() =40.
=40.
∵a=﹣10<0,抛物线开口向下,∴当30≤x≤40时,w≥2000.
∵20≤x≤32,∴当30≤x≤32时,w≥2000.
设每月的成本为P(元),由题意,得:P=20(﹣10x+500)=﹣200x+10000
∵k=﹣200<0,∴P随x的增大而减小,∴当x=32时,P的值最小,P最小值=3600.
答:想要每月获得的利润不低于2000元,小明每月的成本最少为3600元.
-
科目: 来源: 题型:
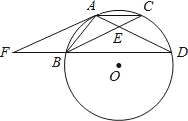
查看答案和解析>>【题目】如图,点A,B,C,D在⊙O上,AB=AC,AD与BC相交于点E,AE=
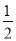 ED,延长DB到点F,使FB=
ED,延长DB到点F,使FB=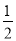 BD,连接AF.
BD,连接AF.(1)证明:△BDE∽△FDA;
(2)试判断直线AF与⊙O的位置关系,并给出证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知O是AB上的一点,从O点引出射线OC、OE、OD,其中OE平分∠BOC.
(1)如图1,若∠COD是直角,∠DOE=15°,求∠AOE的度数;
(2)如图1,若∠AOC=∠BOD,∠DOE=15°,求∠AOE的度数;
(3)将图1中的∠COD (∠COD仍是直角)绕顶点O顺时针旋转至图2的位置,若∠AOC=
 , ∠DOE=
, ∠DOE= ,请猜想
,请猜想 与
与 之间存在什么样的数量关系,写出你的结论,并说明理由.
之间存在什么样的数量关系,写出你的结论,并说明理由. 
-
科目: 来源: 题型:
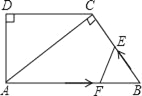
查看答案和解析>>【题目】如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,求y关于t的函数关系式,并求出y的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,是假命题的是( )
A. 过
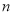 边形一个顶点的所有对角线,将这个多边形分成
边形一个顶点的所有对角线,将这个多边形分成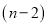 个三角形
个三角形B. 三角形中,到三个顶点距离相等的点是三条边垂直平分线的交点
C. 三角形的中线将三角形分成面积相等的两部分
D. 一组对边平行另一组对边相等的四边形是平行四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
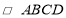 中,
中,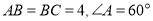 ,连接
,连接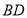 ,将
,将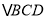 绕点
绕点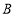 旋转,当
旋转,当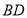 (即
(即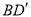 )与
)与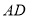 交于一点
交于一点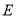 ,
,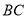 (即
(即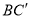 )与
)与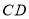 交于一点
交于一点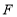 时,给出以下结论:①
时,给出以下结论:①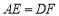 ;②
;②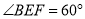 ;③
;③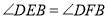 ;④
;④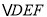 的周长的最小值是
的周长的最小值是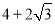 .其中正确的是( )
.其中正确的是( )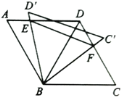
A. ①②③B. ①②④C. ②③④D. ①③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知数轴上
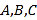 三点对应的数分别为
三点对应的数分别为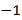 、3、5,点
、3、5,点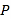 为数轴上任意一点,其对应的数为
为数轴上任意一点,其对应的数为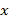 .点
.点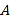 与点
与点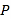 之间的距离表示为
之间的距离表示为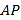 ,点
,点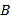 与点
与点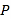 之间的距离表示为
之间的距离表示为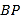 .
.(1)若
 ,则
,则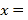 ;
;(2)若
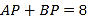 ,求
,求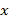 的值;
的值;(3)若点
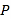 从点
从点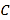 出发,以每秒3个单位的速度向右运动,点
出发,以每秒3个单位的速度向右运动,点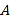 以每秒1个单位的速度向左运动,点
以每秒1个单位的速度向左运动,点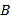 以每秒2个单位的速度向右运动,三点同时出发.设运动时间为
以每秒2个单位的速度向右运动,三点同时出发.设运动时间为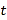 秒,试判断:
秒,试判断: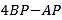 的值是否会随着
的值是否会随着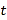 的变化而变化?请说明理由.
的变化而变化?请说明理由.
相关试题

