【题目】抛物线y=﹣x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,3).
(1)求抛物线的解析式;
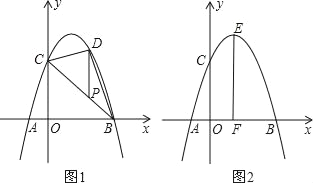
(2)如图1,P为线段BC上一点,过点P作y轴平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
参考答案:
【答案】(1)y=﹣x2+2x+3;(2)当a=![]() 时,△BDC的面积最大,此时P(
时,△BDC的面积最大,此时P(![]() ,
, ![]() );(3)m的变化范围为:﹣
);(3)m的变化范围为:﹣![]() ≤m≤5
≤m≤5
【解析】试题分析:
解:
(1)由题意得:![]() ,解得:
,解得: ![]() ,
,
∴抛物线解析式为![]() ;
;
(2)令![]() ,
,
∴x1= -1,x2=3,即B(3,0),
设直线BC的解析式为y=kx+b′,
∴![]() ,解得:
,解得: ![]() ,
,
∴直线BC的解析式为![]() ,
,
设P(a,3-a),则D(a,-a2+2a+3),
∴PD=(-a2+2a+3)-(3-a)=-a2+3a,
∴S△BDC=S△PDC+S△PDB
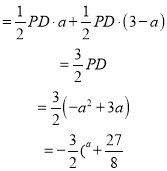 ,
,
∴当![]() 时,△BDC的面积最大,此时P(
时,△BDC的面积最大,此时P(![]() ,
, ![]() );
);
(3)由(1),y=-x2+2x+3=-(x-1)2+4,
∴OF=1,EF=4,OC=3,
过C作CH⊥EF于H点,则CH=EH=1,

当M在EF左侧时,
∵∠MNC=90°,
则△MNF∽△NCH,
∴![]() ,
,
设FN=n,则NH=3-n,
∴![]() ,
,
即n2-3n-m+1=0,
关于n的方程有解,△=(-3)2-4(-m+1)≥0,
得m≥![]() ,
,
当M在EF右侧时,Rt△CHE中,CH=EH=1,∠CEH=45°,即∠CEF=45°,
作EM⊥CE交x轴于点M,则∠FEM=45°,
∵FM=EF=4,
∴OM=5,
即N为点E时,OM=5,
∴m≤5,
综上,m的变化范围为: ![]() ≤m≤5.
≤m≤5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知数轴上
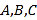 三点对应的数分别为
三点对应的数分别为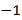 、3、5,点
、3、5,点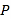 为数轴上任意一点,其对应的数为
为数轴上任意一点,其对应的数为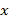 .点
.点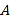 与点
与点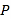 之间的距离表示为
之间的距离表示为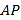 ,点
,点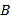 与点
与点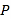 之间的距离表示为
之间的距离表示为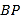 .
.(1)若
 ,则
,则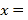 ;
;(2)若
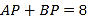 ,求
,求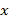 的值;
的值;(3)若点
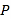 从点
从点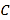 出发,以每秒3个单位的速度向右运动,点
出发,以每秒3个单位的速度向右运动,点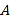 以每秒1个单位的速度向左运动,点
以每秒1个单位的速度向左运动,点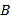 以每秒2个单位的速度向右运动,三点同时出发.设运动时间为
以每秒2个单位的速度向右运动,三点同时出发.设运动时间为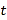 秒,试判断:
秒,试判断: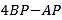 的值是否会随着
的值是否会随着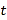 的变化而变化?请说明理由.
的变化而变化?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四边形
 中,
中, ,
, 分别是
分别是 的中点,
的中点, ,则
,则 的长是___________.
的长是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们环保意识的增强,越来越多的人选择低碳出行,各种品牌的山地自行车相继投放市场.顺风车行五月份
 型车的销售总利润为
型车的销售总利润为 元,
元, 型车的销售总利润为
型车的销售总利润为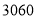 元.且
元.且 型车的销售数量是
型车的销售数量是 型车的
型车的 倍,已知销售
倍,已知销售 型车比
型车比 型车每辆可多获利
型车每辆可多获利 元.
元.(1)求每辆
 型车和
型车和 型车的销售利润;
型车的销售利润;(2)若该车行计划一次购进
 两种型号的自行车共
两种型号的自行车共 台且全部售出,其中
台且全部售出,其中 型车的进货数量不超过
型车的进货数量不超过 型车的
型车的 倍,则该车行购进
倍,则该车行购进 型车、
型车、 型车各多少辆,才能使销售总利润最大?最大销售总利润是多少?
型车各多少辆,才能使销售总利润最大?最大销售总利润是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
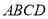 是面积为
是面积为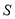 的平行四边形,其中
的平行四边形,其中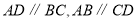 .
.(1)如图①,点
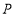 为
为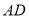 边上任意一点,则
边上任意一点,则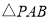 的面积
的面积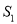 和
和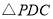 的面积
的面积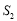 之和与
之和与 的面积
的面积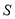 之间的数量关系是__________;
之间的数量关系是__________;(2)如图②,设
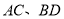 交于点
交于点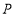 ,则
,则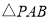 的面积
的面积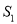 和
和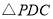 的面积
的面积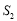 之和与
之和与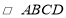 的面积
的面积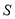 之间的数量关系是___________;
之间的数量关系是___________;(3)如图③,点
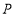 为
为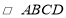 内任意一点时,试猜想
内任意一点时,试猜想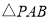 的面积
的面积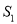 和
和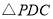 的面积
的面积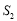 之和与
之和与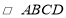 的面积
的面积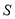 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;(4)如图④,已知点
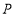 为
为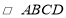 内任意一点,
内任意一点,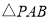 的面积为
的面积为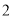 ,
,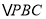 的面积为
的面积为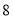 ,连接
,连接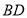 ,求
,求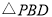 的面积.
的面积.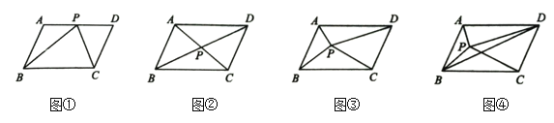
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为1的正方形,E,F为BD所在直线上的两点.若AE=
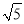 ,∠EAF=135°,则以下结论正确的是( )
,∠EAF=135°,则以下结论正确的是( )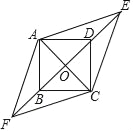
A. DE=1 B. tan∠AFO=
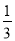 C. AF=
C. AF= D. 四边形AFCE的面积为
D. 四边形AFCE的面积为
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,下列四个结论:
①4a+c<0;②m(am+b)+b>a(m≠﹣1);③关于x的一元二次方程ax2+(b﹣1)x+c=0没有实数根;④ak4+bk2<a(k2+1)2+b(k2+1)(k为常数).其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
相关试题

