【题目】某社区购买甲、乙两种树苗进行绿化,购买一棵甲种树苗的价钱比购买一棵乙种树苗的价钱多 10 元钱,已知购买 20 棵甲种树苗、30 棵乙种树苗共需 1 200 元钱.
(1)求购买一棵甲种、一棵乙种树苗各多少元?
(2)社区决定购买甲、乙两种树苗共 400 棵,总费用不超过 10 600 元,那么该社区最多可以购买多少棵甲种树苗?
参考答案:
【答案】(1)购买一棵甲种树苗需30元,购买一棵乙种树苗需20元;(2)该社区最多可以购买260棵甲种树苗.
【解析】
(1)设出未知数,根据“一棵甲种树苗的价钱比购买一棵乙种树苗的价钱多10元钱;购买 20棵甲种树苗、30棵乙种树苗共需1200元钱”列出方程组,求解即可;
(2)设出未知数,根据两种树苗共买400棵且总费用不超过10600元列出一元一次不等式,然后解不等式即可.
解:(1)设购买一棵甲种树苗需x元,购买一棵乙种树苗需y元,
由题意得:![]() ,
,
解得:![]() ,
,
答:购买一棵甲种树苗需30元,购买一棵乙种树苗需20元;
(2)设该社区购买a棵甲种树苗,则购买(400-a)棵乙种树苗,
由题意得:30a+20(400-a)≤10600,
解得:x≤260,
答:该社区最多可以购买260棵甲种树苗.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场设立了一个可以自由转动的转盘,并做如下规定:顾客购物80元以上就获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品,下表是活动进行中的一组统计数据.

(1)计算并完成表格;
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动该盘一次,你获得洗衣粉的概率约是多少?
(4)在该转盘中,表示“洗衣粉”区域的扇形的圆心角约是多少?(精确到1°)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船的北偏东60°方向上,40分钟后,渔船行至B处,此时看见小岛C在渔船的北偏东30°方向上.

(1)求A处与小岛C之间的距离;
(2)渔船到达B处后,航行方向不变,当渔船继续航行多长时间时,才能与小岛C的距离最短.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.已知:在矩形
 中,
中, 是对角线,
是对角线, 于点
于点 ,
, 于点
于点 ;
;
(1)如图1,求证:
 ;
;(2)如图2,当
 时,连接
时,连接 .
. ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形 面积的
面积的 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(发现)任意三个连续偶数的平方和是4的倍数。
(验证)(1)
 的结果是4的几倍?
的结果是4的几倍?(2)设三个连续偶数的中间一个为
 ,写出它们的平方和,并说明是4的倍数。
,写出它们的平方和,并说明是4的倍数。(延伸)(3)设三个连续奇数的中间一个数为
 ,写出它们的平方和,它是12的倍数吗?若是,说明理由,若不是,写出被12除余数是多少?
,写出它们的平方和,它是12的倍数吗?若是,说明理由,若不是,写出被12除余数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,正方形
 中,点E在
中,点E在 上,点F在
上,点F在 上,连接
上,连接 、
、 、
、 .且
.且 平分
平分 .
.
(1)如图1,求证:
 .
.(2)如图2,若点E为BC的中点,
 ,求
,求 的面积.
的面积.(3)如图3,若∠B=90°,连接BD分别交AF、AE于M、N两点,连接ME,若ME⊥AF于M, BM:EF=4
 :5,△AEF的面积为15时,求AE的长度.
:5,△AEF的面积为15时,求AE的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形
 的顶点O与坐标原点重合,顶点A、C在坐标轴上,
的顶点O与坐标原点重合,顶点A、C在坐标轴上, ,将矩形沿
,将矩形沿 折叠,使点A与点C重合.
折叠,使点A与点C重合.
(1)求点E的坐标;
(2)点P从O出发,沿折线 方向以每秒2个单位的速度匀速运动,到达终点E时停止运动,设P的运动时间为t,
方向以每秒2个单位的速度匀速运动,到达终点E时停止运动,设P的运动时间为t, 的面积为S,求S与t的关系式,直接写出t的取值范围;
的面积为S,求S与t的关系式,直接写出t的取值范围;
(3)在(2)的条件下,当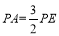 时,在平面直角坐标系中是否存在点Q,使得以点P、E、G、Q为顶点的四边形为平行四边形?若不存在,请说明理由;若存在,请求出点Q的坐标.
时,在平面直角坐标系中是否存在点Q,使得以点P、E、G、Q为顶点的四边形为平行四边形?若不存在,请说明理由;若存在,请求出点Q的坐标.
相关试题

