Question

【题目】如图，在平面直角坐标系中，矩形的顶点O与坐标原点重合，顶点A、C在坐标轴上，，将矩形沿折叠，使点A与点C重合．

（1）求点E的坐标；
（2）点P从O出发，沿折线方向以每秒2个单位的速度匀速运动，到达终点E时停止运动，设P的运动时间为t，的面积为S，求S与t的关系式，直接写出t的取值范围；
（3）在（2）的条件下，当时，在平面直角坐标系中是否存在点Q，使得以点P、E、G、Q为顶点的四边形为平行四边形？若不存在，请说明理由；若存在，请求出点Q的坐标．

Answer 1

【答案】（1）E（10，6）；（2）S= -8t+54（0≤t≤3）或S=-6t+48（3＜t≤8）；（3）存在， Q（14.4，-4.8）或（18.4，-4.8）．

【解析】

（1）设AE=x，根据勾股定理列方程得：（18-x）2+62=x2，解出可得结论；
（2）分两种情况：P在OA或AE上，分别根据三角形面积列式即可；
（3）先根据分别计算PA和PE的长，如图4，过G作GH⊥OC于H，设OF=y，根据勾股定理列方程可得y的值，利用面积法计算GH的长，得G的坐标，根据平行四边形的性质和平移规律可得Q的坐标．

解：（1）如图1，矩形ABCO中，B（18，6），

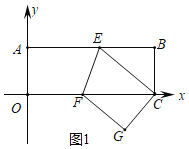
∴AB=18，BC=6，
设AE=x，则EC=x，BE=18-x，
Rt△EBC中，由勾股定理得：EB2+BC2=EC2，
∴（18-x）2+62=x2，
x=10，
即AE=10，
∴E（10，6）；

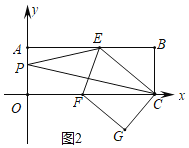
（2）分两种情况：
①当P在OA上时，0≤t≤3，如图2，
S=S矩形OABC-S△PAE-S△BEC-S△OPC，
=18×6-×10（6-2t）-×8×6-×18×2t，
=-8t+54，
②当P在AE上时，3＜t≤8，如图3，

S=PEBC=×6×(162t)=3（16-2t）=-6t+48；
（3）存在，由PA=PE可知：P在AE上，如图4，过G作GH⊥OC于H，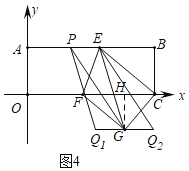

∵AP+PE=10，
∴AP=6，PE=4，
设OF=y，则FG=y，FC=18-y，
由折叠得：∠CGF=∠AOF=90°，
由勾股定理得：FC2=FG2+CG2，
∴（18-y）2=y2+62，
y=8，
∴FG=8，FC=18-8=10，
FCGH＝FGCG，
×10×GH＝×6×8，
GH=4.8，
由勾股定理得：FH==6.4，
∴OH=8+6.4=14.4，
∴G（14.4，-4.8），
∵点P、E、G、Q为顶点的四边形为平行四边形，且PE=4，
∴Q（14.4，-4.8）或（18.4，-4.8）．