【题目】已知,正方形![]() 中,点E在
中,点E在![]() 上,点F在
上,点F在![]() 上,连接
上,连接![]() 、
、![]() 、
、![]() .且
.且![]() 平分
平分![]() .
.

(1)如图1,求证:![]() .
.
(2)如图2,若点E为BC的中点,![]() ,求
,求![]() 的面积.
的面积.
(3)如图3,若∠B=90°,连接BD分别交AF、AE于M、N两点,连接ME,若ME⊥AF于M, BM:EF=4![]() :5,△AEF的面积为15时,求AE的长度.
:5,△AEF的面积为15时,求AE的长度.
参考答案:
【答案】(1)证明见解析;(2)15;(3)2![]() .
.
【解析】
(1)作AH⊥EF于H.只要证明△AFD≌△AFH,推出∠FAD=∠FAH,同法可证:∠EAB=∠EAH,由此即可解决问题;
(2)由△EAB≌△EAH,△FAD≌△FAH,推出BE=EH=3,DF=FH,设DF=FH=x,在Rt△EFC中,根据EF2=EC2+CF2,可得(x+3)2=32+(6-x)2,推出x=2,推出EF=3+2=5,即可解决问题;
(3)如图3中,如图将△ADM顺时针旋转90°得到△ABK.首先证明MN2=BN2+DM2,再证明EF=![]() MN,由BM:EF=4
MN,由BM:EF=4![]() :5,推出BM:
:5,推出BM:![]() MN=4
MN=4![]() :5,推出BM:NM=8:5,设BM=8k,NM=5k,则BN=3k,DM=
:5,推出BM:NM=8:5,设BM=8k,NM=5k,则BN=3k,DM=![]() =4k,由DF∥AB,推出
=4k,由DF∥AB,推出![]() =2,设MF=y,则AM=ME=2y,由
=2,设MF=y,则AM=ME=2y,由![]() AFEM=15,推出
AFEM=15,推出![]() 3b2b=15,可得b=
3b2b=15,可得b=![]() ,由此即可解决问题.
,由此即可解决问题.
(1)证明:作AH⊥EF于H.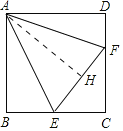
∵四边形ABCD是正方形,
∴∠B=∠D=∠BAD=90°,AB=AD=BC=CD,
∵AE平分∠BEF,AB⊥BE,AH⊥EF,
∴AB=AH=AD,
在Rt△AFD和Rt△AFH中,![]() ,
,
∴△AFD≌△AFH,
∴∠FAD=∠FAH,同法可证:∠EAB=∠EAH,
∴∠EAF=![]() ∠BAH+
∠BAH+![]() ∠DAH=
∠DAH=![]() ×90°=45°.
×90°=45°.
(2)解:∵△EAB≌△EAH,△FAD≌△FAH,
∴BE=EH=3,DF=FH,设DF=FH=x,
在Rt△EFC中,∵EF2=EC2+CF2,
∴(x+3)2=32+(6-x)2,
∴x=2,
∴EF=3+2=5,
∴S△AEF=![]() ×5×6=15.
×5×6=15.
(3)解:如图3中,如图将△ADM顺时针旋转90°得到△ABK.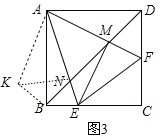
∵∠BAD=90°,∠MAN=45°,
∴∠DAM+∠BAN=45°,
∵∠DAM=∠BAK,
∴∠BAN+∠BAK=45°,
∴∠NAK=∠MAN=45°,
∵AN=AN,AK=AM,
∴△ANK≌△ANM,
∴MN=KN,
∵∠ABK=∠ADM=45°=∠ABD,
∴∠KBN=90°,
∴KN2=BN2+BK2,
∵DM=BK,
∴MN2=BN2+DM2,
∵∠MAN=∠NBE,∠ANM=∠BNE,
∴∠AMN=∠BEN=∠AEF,
∵∠AMN=∠EAF,
∴△AMN∽△AEF,
∴![]() ,
,
∴EF=![]() MN,
MN,
∵BM:EF=4![]() :5,
:5,
∴BM:![]() MN=4
MN=4![]() :5,
:5,
∴BM:NM=8:5,设BM=8k,NM=5k,
则BN=3k,DM=![]() =4k,
=4k,
∵DF∥AB,
∴![]() =2,设MF=y,则AM=ME=2y,
=2,设MF=y,则AM=ME=2y,
∵![]() AFEM=15,
AFEM=15,
∴![]() 3b2b=15,
3b2b=15,
∴b2=5,
∵b>0,
∴b=![]() ,
,
∴AM=EM=2![]() ,
,
∴AE=![]() AM=2
AM=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】.已知:在矩形
 中,
中, 是对角线,
是对角线, 于点
于点 ,
, 于点
于点 ;
;
(1)如图1,求证:
 ;
;(2)如图2,当
 时,连接
时,连接 .
. ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形 面积的
面积的 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某社区购买甲、乙两种树苗进行绿化,购买一棵甲种树苗的价钱比购买一棵乙种树苗的价钱多 10 元钱,已知购买 20 棵甲种树苗、30 棵乙种树苗共需 1 200 元钱.
(1)求购买一棵甲种、一棵乙种树苗各多少元?
(2)社区决定购买甲、乙两种树苗共 400 棵,总费用不超过 10 600 元,那么该社区最多可以购买多少棵甲种树苗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(发现)任意三个连续偶数的平方和是4的倍数。
(验证)(1)
 的结果是4的几倍?
的结果是4的几倍?(2)设三个连续偶数的中间一个为
 ,写出它们的平方和,并说明是4的倍数。
,写出它们的平方和,并说明是4的倍数。(延伸)(3)设三个连续奇数的中间一个数为
 ,写出它们的平方和,它是12的倍数吗?若是,说明理由,若不是,写出被12除余数是多少?
,写出它们的平方和,它是12的倍数吗?若是,说明理由,若不是,写出被12除余数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形
 的顶点O与坐标原点重合,顶点A、C在坐标轴上,
的顶点O与坐标原点重合,顶点A、C在坐标轴上, ,将矩形沿
,将矩形沿 折叠,使点A与点C重合.
折叠,使点A与点C重合.
(1)求点E的坐标;
(2)点P从O出发,沿折线 方向以每秒2个单位的速度匀速运动,到达终点E时停止运动,设P的运动时间为t,
方向以每秒2个单位的速度匀速运动,到达终点E时停止运动,设P的运动时间为t, 的面积为S,求S与t的关系式,直接写出t的取值范围;
的面积为S,求S与t的关系式,直接写出t的取值范围;
(3)在(2)的条件下,当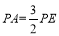 时,在平面直角坐标系中是否存在点Q,使得以点P、E、G、Q为顶点的四边形为平行四边形?若不存在,请说明理由;若存在,请求出点Q的坐标.
时,在平面直角坐标系中是否存在点Q,使得以点P、E、G、Q为顶点的四边形为平行四边形?若不存在,请说明理由;若存在,请求出点Q的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
求证:(1)△ABD≌△ACD;
(2)BE=CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁4名同学进行一次羽毛球单打比赛,要从中选出2名同学举行首场比赛.求下列事件的概率:
(1)已确定甲打第一场,再从其余3名同学中随机选取1名,恰好选中乙同学.
(2)随机选取2名同学,其中有乙同学.
相关试题

