【题目】(1)如图(1)在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:DE=BD+CE;
(2)如图(2)将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请给出证明;若不成立,请说明理由.

参考答案:
【答案】(1)见解析;(2)成立,理由见解析
【解析】
(1)根据AAS证明△ADB≌△CEA,得到AE=BD,AD=CE,即可证明;
(2)同理证明△ADB≌△CEA,得到AE=BD,AD=CE,即可证明;
证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中,
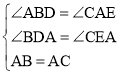 ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中,
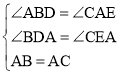 ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下。(单位:km)

(1)在第几次记录时离A地最远,并求出最远距离。
(2)求收工时距A地多远?在A地的什么方向?
(3)若每千米耗油0.3升,问共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的结论是( )
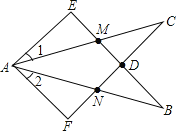
A.CD=DN;B.∠1=∠2;C.BE=CF;D.△ACN≌△ABM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】说理填空:如图,点E是DC的中点,EC=EB,∠CDA=120°,DF//BE,且DF平分∠CDA,若△BCE的周长为18cm,求DC的长.
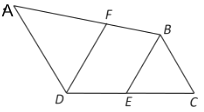
解: 因为DF平分∠CDA,(已知)
所以∠FDC=
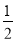 ∠_________.(____________________)
∠_________.(____________________)因为∠CDA=120°,(已知)所以∠FDC=______°.
因为DF//BE,(已知)
所以∠FDC=∠_________=60°.(____________________________________)
又因为EC=EB,(已知)
所以△BCE为等边三角形.(________________________________________)
因为△BCE的周长为18cm,(已知) 所以BE=EC=BC=6 cm.
因为点E是DC的中点,(已知) 所以DC=2EC=12 cm .
-
科目: 来源: 题型:
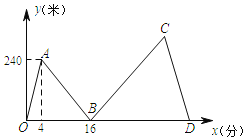
查看答案和解析>>【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人间的距离y(米)与甲出发的时间x(分)之间的关系如图中折线OA-AB-BC-CD所示.
(1)求线段AB的表达式,并写出自变量x的取值范围;
(2)求乙的步行速度;
(3)求乙比甲早几分钟到达终点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的平面直角坐标系(每格的宽度为1)中,已知点A的坐标是
 ,点B的坐标是
,点B的坐标是 ,
,

(1)在直角坐标平面中画出线段AB;
(2)B点到原点O的距离是 ;
(3)将线段AB沿
 轴的正方向平移4个单位,画出平移后的线段A1BI,并写出点A1、B1的坐标.
轴的正方向平移4个单位,画出平移后的线段A1BI,并写出点A1、B1的坐标.(4)求△A1B B1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AM=CM,AD=CD,DM//BC,判断△CMB的形状,并说明理由.

相关试题

