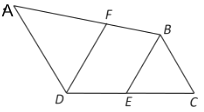
【题目】如图,∠E=∠F=90°,∠B=∠C,AE=AF,下列结论不正确的结论是( )
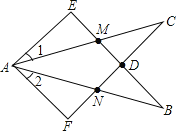
A.CD=DN;B.∠1=∠2;C.BE=CF;D.△ACN≌△ABM.
参考答案:
【答案】A
【解析】
利用“角角边”证明△ABE和△ACF全等,根据全等三角形对应角相等可得∠BAE=∠CAF,然后求出∠1=∠2,全等三角形对应边相等可得BE=CF,AB=AC,再利用“角边角”证明△ACN和△ABM全等.
在△ABE和△ACF中,
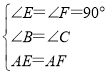 ,
,
∴△ABE≌△ACF(AAS),
∴∠BAE=∠CAF,BE=CF,AB=AC,故C选项结论正确;
∴∠BAE-∠BAC=∠CAF-∠BAC,
即∠1=∠2,故B选项结论正确;
在△ACN和△ABM中,
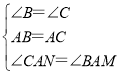 ,
,
∴△ACN≌△ABM(ASA),故D选项结论正确;
CD与DN的大小无法确定,故A选项结论错误.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农户承包荒山若干亩种植脐橙,投资59000元种植脐橙果树4000棵;今年脐橙总产量预测为60000千克,脐橙在市场上每千克售a元,在果园每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售2000千克,需4人帮忙,每人每天付工资100元,农用车运费及其他各项税费平均每天300元.
(1)分别用a,b表示两种方式出售水果的收入?
(2)若a=2.5元,b=2元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好?
(3)该农户加强果园管理,力争到明年纯收入达到84000元,而且该农户采用了(2)中较好的出售方式出售,那么纯收入增长率是多少(纯收入=总收入﹣总支出)?
-
科目: 来源: 题型:
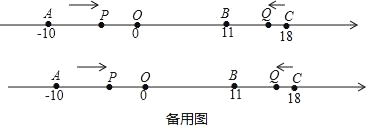
查看答案和解析>>【题目】如图,在数轴上,点A表示﹣10,点B表示11,点C表示18.动点P从点A出发,沿数轴正方向以每秒2个单位的速度匀速运动;同时,动点Q从点C出发,沿数轴负方向以每秒1个单位的速度匀速运动.设运动时间为t秒.
(1)当t为何值时,P、Q两点相遇?相遇点M所对应的数是多少?
(2)在点Q出发后到达点B之前,求t为何值时,点P到点O的距离与点Q到点B的距离相等;
(3)在点P向右运动的过程中,N是AP的中点,在点P到达点C之前,求2CN﹣PC的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某检修小组从A地出发,在东西向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶记录如下。(单位:km)

(1)在第几次记录时离A地最远,并求出最远距离。
(2)求收工时距A地多远?在A地的什么方向?
(3)若每千米耗油0.3升,问共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】说理填空:如图,点E是DC的中点,EC=EB,∠CDA=120°,DF//BE,且DF平分∠CDA,若△BCE的周长为18cm,求DC的长.
解: 因为DF平分∠CDA,(已知)
所以∠FDC=
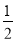 ∠_________.(____________________)
∠_________.(____________________)因为∠CDA=120°,(已知)所以∠FDC=______°.
因为DF//BE,(已知)
所以∠FDC=∠_________=60°.(____________________________________)
又因为EC=EB,(已知)
所以△BCE为等边三角形.(________________________________________)
因为△BCE的周长为18cm,(已知) 所以BE=EC=BC=6 cm.
因为点E是DC的中点,(已知) 所以DC=2EC=12 cm .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1)在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:DE=BD+CE;
(2)如图(2)将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请给出证明;若不成立,请说明理由.

-
科目: 来源: 题型:
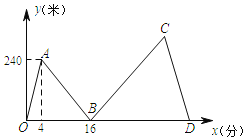
查看答案和解析>>【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人间的距离y(米)与甲出发的时间x(分)之间的关系如图中折线OA-AB-BC-CD所示.
(1)求线段AB的表达式,并写出自变量x的取值范围;
(2)求乙的步行速度;
(3)求乙比甲早几分钟到达终点?
相关试题

