搜索
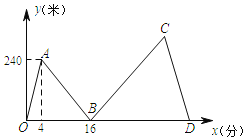
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米，先到终点的人原地休息．已知甲先出发4分钟，在整个步行过程中，甲、乙两人间的距离y(米)与甲出发的时间x(分)之间的关系如图中折线OA-AB-BC-CD所示．
(1)求线段AB的表达式，并写出自变量x的取值范围；
(2)求乙的步行速度；
(3)求乙比甲早几分钟到达终点？
参考答案：
【答案】（1）
；（2）80米/分；（3）6分钟
【解析】
（1）根据图示，设线段AB的表达式为：y=kx+b，把把（4，240），（16，0）代入得到关于k，b的二元一次方程组，解之，即可得到答案，
（2）根据线段OA，求出甲的速度，根据图示可知：乙在点B处追上甲，根据速度=路程÷时间，计算求值即可，
（3）根据图示，求出二者相遇时与出发点的距离，进而求出与终点的距离，结合（2）的结果，分别计算出相遇后，到达终点甲和乙所用的时间，二者的时间差即可所求答案．
（1）根据题意得：
设线段AB的表达式为：y=kx+b （4≤x≤16），
把（4，240），（16，0）代入得：
，
解得：
，
即线段AB的表达式为：y= -20x+320 （4≤x≤16），
（2）又线段OA可知：甲的速度为：
=60（米/分），
乙的步行速度为：
=80（米/分），
答：乙的步行速度为80米/分，
（3）在B处甲乙相遇时，与出发点的距离为：240+（16-4）×60=960（米），
与终点的距离为：2400-960=1440（米），
相遇后，到达终点甲所用的时间为：
=24（分），
相遇后，到达终点乙所用的时间为：
=18（分），
24-18=6（分），
答：乙比甲早6分钟到达终点．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠E=∠F=90°，∠B=∠C，AE=AF，下列结论不正确的结论是（ ）
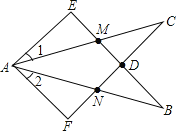
A.CD=DN；B.∠1=∠2；C.BE=CF；D.△ACN≌△ABM．
-
科目： 来源： 题型：
查看答案和解析>>【题目】说理填空：如图，点E是DC的中点，EC=EB，∠CDA=120°，DF//BE，且DF平分∠CDA，若△BCE的周长为18cm，求DC的长．
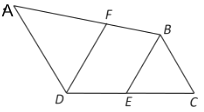
解： 因为DF平分∠CDA,（已知）
所以∠FDC=
∠_________.（____________________）因为∠CDA=120°,（已知）所以∠FDC=______°.
因为DF//BE,（已知）
所以∠FDC=∠_________=60°.（____________________________________）
又因为EC=EB,（已知）
所以△BCE为等边三角形.（________________________________________）
因为△BCE的周长为18cm,（已知） 所以BE=EC=BC=6 cm.
因为点E是DC的中点,（已知） 所以DC=2EC=12 cm .
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）如图（1）在△ABC中，∠BAC＝90°，AB＝AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．求证：DE＝BD+CE；
（2）如图（2）将（1）中的条件改为：在△ABC中，AB＝AC，D、A、E三点都在直线m上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问结论DE＝BD+CE是否成立？如成立，请给出证明；若不成立，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在如图所示的平面直角坐标系（每格的宽度为1）中，已知点A的坐标是
，点B的坐标是
，
（1）在直角坐标平面中画出线段AB；
（2）B点到原点O的距离是 ；
（3）将线段AB沿
轴的正方向平移4个单位，画出平移后的线段A1BI，并写出点A1、B1的坐标．（4）求△A1B B1的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AM=CM，AD=CD，DM//BC，判断△CMB的形状，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在校园文化艺术节中，九年级一班有1名男生和2名女生获得美术奖，另有2名男生和2名女生获得音乐奖．
（1）从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会，求刚好是男生的概率；
（2）分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会，用列表或树状图求刚好是一男生一女生的概率．
相关试题
