【题目】如图,已知一条直线过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,其中点
两点,其中点![]() 的横坐标是
的横坐标是![]() .
.

![]() 求这条直线的函数关系式及点
求这条直线的函数关系式及点![]() 的坐标.
的坐标.
![]() 在
在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
![]() 过线段
过线段![]() 上一点
上一点![]() ,作
,作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,点
,点![]() 在第一象限,点
在第一象限,点![]() ,当点
,当点![]() 的横坐标为何值时,
的横坐标为何值时,![]() 的长度最大?最大值是多少?
的长度最大?最大值是多少?
参考答案:
【答案】(1) 直线![]() ,B(8,16);(2)存在,
,B(8,16);(2)存在,![]() 或
或![]() ,理由见解析;(3)当
,理由见解析;(3)当![]() 的横坐标为
的横坐标为![]() 时,
时,![]() 的长度的最大值是
的长度的最大值是![]()
【解析】
(1)首先求得点A的坐标,然后利用待定系数法确定直线的解析式,从而求得直线与抛物线的交点坐标;
(2)如图1,过点B作BG∥x轴,过点A作AG∥y轴,交点为G,然后分若∠BAC=90°,则AB2+AC2=BC2;若∠ACB=90°,则AB2=AC2+BC2;若∠ABC=90°,则AB2+BC2=AC2三种情况求得m的值,从而确定点C的坐标;
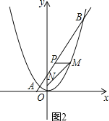
(3)设M(a,![]() a2),如图2,设MP与y轴交于点Q,首先在Rt△MQN中,由勾股定理得MN=
a2),如图2,设MP与y轴交于点Q,首先在Rt△MQN中,由勾股定理得MN=![]() a2+1,然后根据点P与点M纵坐标相同得到x=
a2+1,然后根据点P与点M纵坐标相同得到x=![]() ,从而得到MN+3PM=-
,从而得到MN+3PM=-![]() a2+3a+9,确定二次函数的最值即可.
a2+3a+9,确定二次函数的最值即可.
解:![]() ∵点
∵点![]() 是直线与抛物线的交点,且横坐标为
是直线与抛物线的交点,且横坐标为![]() ,
,
∴![]() ,
,![]() 点的坐标为
点的坐标为![]() ,
,
设直线的函数关系式为![]() ,
,
将![]() ,
,![]() 代入得
代入得![]() ,
,
解得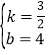 ,
,
∴直线![]() ,
,
∵直线与抛物线相交,
∴![]() ,
,
解得:![]() 或
或![]() ,
,
当![]() 时,
时,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ;
;
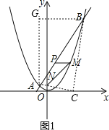
![]() 如图
如图![]() ,过点
,过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,交点为
轴,交点为![]() ,
,
∴![]() ,
,
∵由![]() ,
,![]() 可求得
可求得![]() .
.
设点![]() ,同理可得
,同理可得![]() ,
,
![]() ,
,
①若![]() ,则
,则![]() ,即
,即![]() ,
,
解得:![]() ;
;
②若![]() ,则
,则![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() ;
;
③若![]() ,则
,则![]() ,即
,即![]() ,
,
解得:![]() ;
;
∴点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() ,
,![]() 设
设![]() ,如图
,如图![]() ,设
,设![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
又∵点![]() 与点
与点![]() 纵坐标相同,
纵坐标相同,
∴![]() ,
,
∴![]() ,
,
∴点![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当![]() ,
,
又∵![]() ,
,
∴取到最小值![]() ,
,
∴当![]() 的横坐标为
的横坐标为![]() 时,
时,![]() 的长度的最大值是
的长度的最大值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
阅读下列材料:
配方法是初中数学中经常用到的一个重要方法,学好配方法对我们学习数学有很大的帮助,所谓配方就是将某一个多项式变形为一个完全平方式,变形一定要是恒等的,例如解方程
 ,则
,则 ,∴
,∴
求
 、
、 .则有
.则有 ,∴
,∴ .解得
.解得 ,
, .
. 则有
则有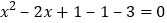 ,∴
,∴ .解得
.解得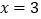 或
或 ,根据以上材料解答下列各题:
,根据以上材料解答下列各题: 若
若 .求
.求 的值.
的值. .求
.求 的值.
的值. 若
若 .求
.求 的值.
的值. 若
若 ,
, ,
, 表示
表示 的三边,且
的三边,且 ,试判断
,试判断 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数
 的图象如图所示,则下列说法中正确的是( )
的图象如图所示,则下列说法中正确的是( )
A.
 B.
B. 
C. 当
 时,
时, 随
随 的增大而减小 D.
的增大而减小 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款
 元,第三天收到捐款
元,第三天收到捐款 元.
元. 如果第二天、第三天收到捐款的增长率相同,求捐款增长率?
如果第二天、第三天收到捐款的增长率相同,求捐款增长率? 按照
按照 中收到捐款的增长率不变,该单位三天一共能收到多少捐款?
中收到捐款的增长率不变,该单位三天一共能收到多少捐款? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线


 求该抛物线的对称轴和顶点坐标;
求该抛物线的对称轴和顶点坐标; 求抛物线与
求抛物线与 轴交点的坐标;
轴交点的坐标; 画出抛物线的示意图;
画出抛物线的示意图; 根据图象回答:当
根据图象回答:当 在什么范围时,
在什么范围时, 随
随 的增大而增大?当
的增大而增大?当 在什么范围时,
在什么范围时, 随
随 的增大而减小?
的增大而减小? 根据图象回答:当
根据图象回答:当 为何值时,
为何值时, ;当
;当 为何值时,
为何值时, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为
 米的篱笆围成.已知墙长为
米的篱笆围成.已知墙长为 米(如图),设这个苗圃园垂直于墙的一边长为
米(如图),设这个苗圃园垂直于墙的一边长为 米.
米.
 若苗圃园的面积为
若苗圃园的面积为 平方米,求
平方米,求 ;
; 若平行于墙的一边长不小于
若平行于墙的一边长不小于 米,这个苗圃园的面积有最大值吗?如果有,求出最大值;如果没有,请说明理由.
米,这个苗圃园的面积有最大值吗?如果有,求出最大值;如果没有,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中,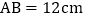 ,
, ,点
,点 从
从 开始沿折线
开始沿折线 以
以 的速度运动,点
的速度运动,点 从
从 开始沿
开始沿 边以
边以 的速度移动,如果点
的速度移动,如果点 、
、 分别从
分别从 、
、 同时出发,当其中一点到达
同时出发,当其中一点到达 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为 ,当
,当 ________时,四边形
________时,四边形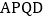 也为矩形.
也为矩形.
相关试题

