【题目】二次函数![]() 的图象如图所示,则下列说法中正确的是( )
的图象如图所示,则下列说法中正确的是( )

A. ![]() B.
B. ![]()
C. 当![]() 时,
时,![]() 随
随![]() 的增大而减小 D.
的增大而减小 D. ![]()
参考答案:
【答案】D
【解析】
A、由抛物线的开口方向,抛物线与y轴交点的位置即可确定a、c的符号;
B、根据抛物线与x轴的交点即可求得抛物线的对称轴,然后把x=2代入方程即可求得相应的y的符号;
C、根据抛物线的对称轴和抛物线图象直接回答;
D、把x=m代入函数解析式中表示出对应的函数值,把x=1代入解析式得到对应的解析式,根据图形可知x=1时函数值最小,所以x=1对应的函数值小于x=m对应的函数值,化简得到不等式成立.
A、根据图示知,抛物线开口方向向上,抛物线与y轴交与负半轴,则a>0,c<0,所以ac<0.故本选项错误;
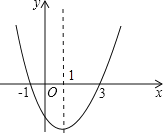
B、根据题意可以求得对称轴x=1,则当x=2时,y<0,即4a+2b+c<0.故本选项错误;
C、根据图示知,当x>1时,y随x的增大而增大.故本选项错误;
D、x=m对应的函数值为y=am2+bm+c,
x=1对应的函数值为y=a+b+c,又x=1时函数取得最小值,
∴a+b+c<am2+bm+c,即a+b<am2+bm=m(am+b),
故本选项正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?

-
科目: 来源: 题型:
查看答案和解析>>【题目】把边长相等的正五边形ABGHI和正六边形ABCDEF的AB边重合,按照如图的方式叠合在一起,连接EB,交HI于点K,则∠BKI的大小为( )

A.90°B.84°C.72°D.88°
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
阅读下列材料:
配方法是初中数学中经常用到的一个重要方法,学好配方法对我们学习数学有很大的帮助,所谓配方就是将某一个多项式变形为一个完全平方式,变形一定要是恒等的,例如解方程
 ,则
,则 ,∴
,∴
求
 、
、 .则有
.则有 ,∴
,∴ .解得
.解得 ,
, .
. 则有
则有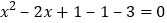 ,∴
,∴ .解得
.解得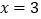 或
或 ,根据以上材料解答下列各题:
,根据以上材料解答下列各题: 若
若 .求
.求 的值.
的值. .求
.求 的值.
的值. 若
若 .求
.求 的值.
的值. 若
若 ,
, ,
, 表示
表示 的三边,且
的三边,且 ,试判断
,试判断 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款
 元,第三天收到捐款
元,第三天收到捐款 元.
元. 如果第二天、第三天收到捐款的增长率相同,求捐款增长率?
如果第二天、第三天收到捐款的增长率相同,求捐款增长率? 按照
按照 中收到捐款的增长率不变,该单位三天一共能收到多少捐款?
中收到捐款的增长率不变,该单位三天一共能收到多少捐款? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一条直线过点
 ,且与抛物线
,且与抛物线 交于
交于 ,
, 两点,其中点
两点,其中点 的横坐标是
的横坐标是 .
.
 求这条直线的函数关系式及点
求这条直线的函数关系式及点 的坐标.
的坐标. 在
在 轴上是否存在点
轴上是否存在点 ,使得
,使得 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由. 过线段
过线段 上一点
上一点 ,作
,作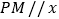 轴,交抛物线于点
轴,交抛物线于点 ,点
,点 在第一象限,点
在第一象限,点 ,当点
,当点 的横坐标为何值时,
的横坐标为何值时, 的长度最大?最大值是多少?
的长度最大?最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线


 求该抛物线的对称轴和顶点坐标;
求该抛物线的对称轴和顶点坐标; 求抛物线与
求抛物线与 轴交点的坐标;
轴交点的坐标; 画出抛物线的示意图;
画出抛物线的示意图; 根据图象回答:当
根据图象回答:当 在什么范围时,
在什么范围时, 随
随 的增大而增大?当
的增大而增大?当 在什么范围时,
在什么范围时, 随
随 的增大而减小?
的增大而减小? 根据图象回答:当
根据图象回答:当 为何值时,
为何值时, ;当
;当 为何值时,
为何值时, .
.
相关试题

