【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为![]() 米的篱笆围成.已知墙长为
米的篱笆围成.已知墙长为![]() 米(如图),设这个苗圃园垂直于墙的一边长为
米(如图),设这个苗圃园垂直于墙的一边长为![]() 米.
米.

![]() 若苗圃园的面积为
若苗圃园的面积为![]() 平方米,求
平方米,求![]() ;
;
![]() 若平行于墙的一边长不小于
若平行于墙的一边长不小于![]() 米,这个苗圃园的面积有最大值吗?如果有,求出最大值;如果没有,请说明理由.
米,这个苗圃园的面积有最大值吗?如果有,求出最大值;如果没有,请说明理由.
参考答案:
【答案】(1)13;(2)若平行于墙的一边长不小于![]() 米,这个苗圃园的面积有最大值,最大值是
米,这个苗圃园的面积有最大值,最大值是![]() 平方米
平方米
【解析】
(1)根据题意可以得到关于x的一元二次方程,从而可以解答本题,注意平行于墙的一般长不能超过18米;
(2)根据题意可以的熬S关于x的二次函数,从而可以解答本题.
![]() 由题意可得,
由题意可得,
![]() ,
,
解得,![]() ,
,![]() ,
,
当![]() 时,平行于墙的边长为
时,平行于墙的边长为![]() ,故
,故![]() 不和题意,应舍去,
不和题意,应舍去,
当![]() 时,平行于墙的边长为
时,平行于墙的边长为![]() ,符合题意,
,符合题意,
即![]() 的值是
的值是![]() ;
;
![]() 若平行于墙的一边长不小于
若平行于墙的一边长不小于![]() 米,这个苗圃园的面积有最大值,最大值是
米,这个苗圃园的面积有最大值,最大值是![]() 平方米,
平方米,
理由:设矩形的面积为![]() 平方米,
平方米,
则![]() ,
,
∵![]() ,
,
解得,![]() ,
,
∴当![]() 时,
时,![]() 取得最大值,此时
取得最大值,此时![]() ,
,
即若平行于墙的一边长不小于![]() 米,这个苗圃园的面积有最大值,最大值是
米,这个苗圃园的面积有最大值,最大值是![]() 平方米.
平方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款
 元,第三天收到捐款
元,第三天收到捐款 元.
元. 如果第二天、第三天收到捐款的增长率相同,求捐款增长率?
如果第二天、第三天收到捐款的增长率相同,求捐款增长率? 按照
按照 中收到捐款的增长率不变,该单位三天一共能收到多少捐款?
中收到捐款的增长率不变,该单位三天一共能收到多少捐款? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一条直线过点
 ,且与抛物线
,且与抛物线 交于
交于 ,
, 两点,其中点
两点,其中点 的横坐标是
的横坐标是 .
.
 求这条直线的函数关系式及点
求这条直线的函数关系式及点 的坐标.
的坐标. 在
在 轴上是否存在点
轴上是否存在点 ,使得
,使得 是直角三角形?若存在,求出点
是直角三角形?若存在,求出点 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由. 过线段
过线段 上一点
上一点 ,作
,作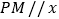 轴,交抛物线于点
轴,交抛物线于点 ,点
,点 在第一象限,点
在第一象限,点 ,当点
,当点 的横坐标为何值时,
的横坐标为何值时, 的长度最大?最大值是多少?
的长度最大?最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线


 求该抛物线的对称轴和顶点坐标;
求该抛物线的对称轴和顶点坐标; 求抛物线与
求抛物线与 轴交点的坐标;
轴交点的坐标; 画出抛物线的示意图;
画出抛物线的示意图; 根据图象回答:当
根据图象回答:当 在什么范围时,
在什么范围时, 随
随 的增大而增大?当
的增大而增大?当 在什么范围时,
在什么范围时, 随
随 的增大而减小?
的增大而减小? 根据图象回答:当
根据图象回答:当 为何值时,
为何值时, ;当
;当 为何值时,
为何值时, .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中,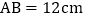 ,
, ,点
,点 从
从 开始沿折线
开始沿折线 以
以 的速度运动,点
的速度运动,点 从
从 开始沿
开始沿 边以
边以 的速度移动,如果点
的速度移动,如果点 、
、 分别从
分别从 、
、 同时出发,当其中一点到达
同时出发,当其中一点到达 时,另一点也随之停止运动,设运动时间为
时,另一点也随之停止运动,设运动时间为 ,当
,当 ________时,四边形
________时,四边形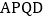 也为矩形.
也为矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠ABC的平分线与在∠ACE的平分线相交于点D.已知∠ABC=70°,∠ACB=30°,求∠A和∠D的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图将两张长为
 ,宽为
,宽为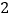 的矩形纸条交叉,重叠部分是一个特殊四边形,则这个特殊四边形周长的最小值为________.
的矩形纸条交叉,重叠部分是一个特殊四边形,则这个特殊四边形周长的最小值为________.
相关试题

