【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,D 是 AC 边上一动点, CE⊥BD 于 E.
(1)如图(1),若 BD 平分∠ABC 时,①求∠ECD 的度数;②求证:BD=2EC;
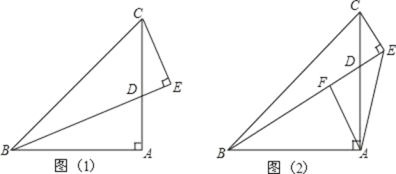
(2)如图(2),过点 A 作 AF⊥BE 于点 F,猜想线段 BE,CE,AF 之间的数量关系并证明你的猜想.
参考答案:
【答案】(1)①22.5°;②见解析;(2) BE﹣CE=2AF,理由见解析.
【解析】
(1)①根据等腰直角三角形的性质得出∠CBA=45![]() ,再利用角平分线的定义解答即可;
,再利用角平分线的定义解答即可;
②延长CE交BA的延长线于点G得出CE=GE,再利用AAS证明ΔABD≌ΔACG,利用全等三角形的性质解答即可;
(2)过点A作AH⊥AE,交BE于点H,证明ΔABH≌ΔACE,进而得出CE=BH,利用等腰直角三角形的判定和性质解答即可.
解:(1)①∵在△ABC 中,∠BAC=90°,AB=AC,
∴∠CBA=45°,
∵BD 平分∠ABC,
∴∠DBA=22.5°,
∵CE⊥BD,
∴∠ECD+∠CDE=90°,∠DBA+∠BDA=90°,
∵∠CDE=∠BDA,
∴∠ECD=∠DBA=22.5°;
②延长 CE 交 BA 的延长线于点 G,如图 1:
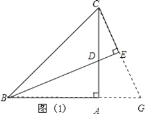
∵BD 平分∠ABC,CE⊥BD,
∴CE=GE,
在△ABD 与△ACG 中,
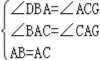 ,
,
∴△ABD≌△ACG(AAS),
∴BD=CG=2CE;
(2)结论:BE﹣CE=2AF.
过点 A 作 AH⊥AE,交 BE 于点 H,如图 2:
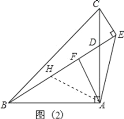
∵AH⊥AE,
∴∠BAH+∠HAC=∠HAC+∠CAE,
∴∠BAH=∠CAE,
在△ABH 与△ACE 中,
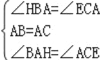
∴△ABH≌△ACE(ASA),
∴CE=BH,AH=AE,
∴△AEH 是等腰直角三角形,
∴AF=EF=HF,
∴BE﹣CE=2AF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,∠BAC=60°,点0是△ABC内一点,△AB0
 △ACD,连接OD.
△ACD,连接OD.(1)求证△AOD为等边三角形。
(2)如图2,连接OC,若∠BOC=130°,∠AOB=
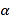 .
.①求∠OCD的度数
②当△OCD是等腰三角形时,求∠
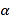 的度数
的度数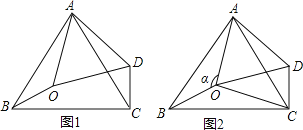 、
、 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上A,B两点对应的数分别为a,b,且a,b满足|a+20|=﹣(b﹣13)2,点C对应的数为16,点D对应的数为﹣13.
(1)求a,b的值;
(2)点A,B沿数轴同时出发相向匀速运动,点A的速度为6个单位/秒,点B的速度为2个单位/秒,若t秒时点A到原点的距离和点B到原点的距离相等,求t的值;
(3)在(2)的条件下,点A,B从起始位置同时出发.当A点运动到点C时,迅速以原来的速度返回,到达出发点后,又折返向点C运动.B点运动至D点后停止运动,当B停止运动时点A也停止运动.求在此过程中,A,B两点同时到达的点在数轴上对应的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某化工车间发生有害气体泄漏,自泄漏开始到完全控制利用了40min,之后将对泄漏有害气体进行清理,线段DE表示气体泄漏时车间内危险检测表显示数据y与时间x(min)之间的函数关系(0≤x≤40),反比例函数y=
 对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:
对应曲线EF表示气体泄漏控制之后车间危险检测表显示数据y与时间x(min)之间的函数关系(40≤x≤?).根据图象解答下列问题:(1)危险检测表在气体泄漏之初显示的数据是 ;
(2)求反比例函数y=
 的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
的表达式,并确定车间内危险检测表恢复到气体泄漏之初数据时对应x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程.
如图:在四边形ABCD中,
 ,
,  于点D,
于点D,  于点F,求证:
于点F,求证: 

证明:
 (已知)
(已知)
 AD// ( )
AD// ( ) = ( )
= ( ) ,
,  (已知)
(已知)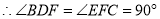 ( )
( ) BD// ( )
BD// ( ) = ( )
= ( )
 ( )
( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中是真命题的是( )
A. 有两边和其中一边的对角对应相等的两个三角形全等
B. 两条平行直线被第三条直线所截,则一组同旁内角的平分线互相垂直
C. 三角形的一个外角等于两个内角的和
D. 等边三角形既是中心对称图形,又是轴对称图形
相关试题

