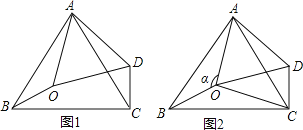
【题目】如图1,在△ABC中,∠BAC=60°,点0是△ABC内一点,△AB0![]() △ACD,连接OD.
△ACD,连接OD.
(1)求证△AOD为等边三角形。
(2)如图2,连接OC,若∠BOC=130°,∠AOB=![]() .
.
①求∠OCD的度数
②当△OCD是等腰三角形时,求∠![]() 的度数
的度数
 、
、
参考答案:
【答案】(1)见解析;.(2)①∠OCD=70°;②可以是130°,100°,115°.
【解析】
(1)根据全等三角形得到AO=AD,∠BAO=∠CAD,由∠BAC=60°,求得∠OAD=60°,即可得到结论;
(2)①根据△AOD为等边三角形,求得∠AOD=∠ADO=60°,求得∠DOC=360°-α-130°-60°=170°-α,根据全等三角形的性质得到∠ADC=∠AOB=α,于是得到∠OCD=180°-∠DOC-∠ODC=70°;②当△OCD是等腰三角形时,(Ⅰ)当OD=OC,由∠DOC=170°-α,得到∠OCD=∠ODC= ![]() α+5°,列方程得到α=130°(Ⅱ)当OD=CD,于是得到∠OCD=∠COD=170°-α;求得∠ODC=180°-2×170°+2α=2α-160°,列方程即可得到α=100°;(Ⅲ)当OC=CD,于是得到∠ODC=∠COD=170°-α,列方程即可得到α=115°.
α+5°,列方程得到α=130°(Ⅱ)当OD=CD,于是得到∠OCD=∠COD=170°-α;求得∠ODC=180°-2×170°+2α=2α-160°,列方程即可得到α=100°;(Ⅲ)当OC=CD,于是得到∠ODC=∠COD=170°-α,列方程即可得到α=115°.
(1)证明:∵△ABO≌△ACD
∴∠OAB=∠CAD
∴AO=AD
∴∠OAB+∠OAC=∠OAC+∠CAD=60°
△AOD为等边三角形.
(2)①∵△AOD为等边三角形,
∴∠AOD=∠ADO=60°,
∵∠BOC=130°,∠AOB=∠α,
∴∠DOC=360°α130°60°=170°α,
∵△ABO≌△ACD,
∴∠ADC=∠AOB=α,
∴∠ODC=α60°,
∴∠OCD=180°∠DOC∠ODC=70°;
②当△OCD是等腰三角形时,
(Ⅰ)当OD=OC,∵∠DOC=170°α,
∴∠OCD=∠ODC=![]() α+5°,
α+5°,
∴60°+![]() α+5°=α,
α+5°=α,
解得:α=130°
(Ⅱ)当OD=CD,∴∠OCD=∠COD=170°α;
∴∠ODC=180°2×170°+2α=2α160°,
∴60°+2α160°=α,
解得:α=100°;
(Ⅲ)当OC=CD,∴∠ODC=∠COD=170°α,
∴170°α+60°=α,
解得:α=115°.
综上所述:当△OCD是等腰三角形时,∠α的度数为:130°,100°,115°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC的三个顶点坐标分别为A(﹣1,﹣2),B(﹣1,﹣4),C(2,﹣3).
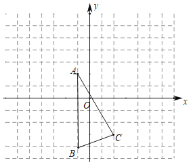
(1)将△ABC先向右平移4个单位,再向上平移6个单位,得到△A1B1C1,作出△A1B1C1,线段AC在平移过程中扫的面积为 ;
(2)作出△A1B1C1关于y轴对称的图形△A2B2C2,则坐标C2为 ;
(3)若△ABD与△ABC全等,则点D的坐标为 (点C与点D不重合)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.
⑴若∠AFD=155°,求∠EDF的度数;
⑵若点F是AC的中点,求证:∠CFD=
 ∠B.
∠B.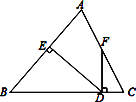
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司经销甲种型号电脑,每台售价4000元.为了增加收入,电脑公司决定再经销乙种型号电脑.已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台.
(1)有几种进货方案?
(2)如果乙种电脑每台售价为3800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金a元,要使(2)中所有方案获利相同,a值应是多少? 若考虑投入成本最低,则应选择哪种进货方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上A,B两点对应的数分别为a,b,且a,b满足|a+20|=﹣(b﹣13)2,点C对应的数为16,点D对应的数为﹣13.
(1)求a,b的值;
(2)点A,B沿数轴同时出发相向匀速运动,点A的速度为6个单位/秒,点B的速度为2个单位/秒,若t秒时点A到原点的距离和点B到原点的距离相等,求t的值;
(3)在(2)的条件下,点A,B从起始位置同时出发.当A点运动到点C时,迅速以原来的速度返回,到达出发点后,又折返向点C运动.B点运动至D点后停止运动,当B停止运动时点A也停止运动.求在此过程中,A,B两点同时到达的点在数轴上对应的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,D 是 AC 边上一动点, CE⊥BD 于 E.
(1)如图(1),若 BD 平分∠ABC 时,①求∠ECD 的度数;②求证:BD=2EC;
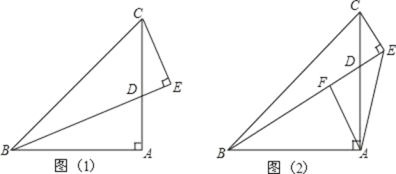
(2)如图(2),过点 A 作 AF⊥BE 于点 F,猜想线段 BE,CE,AF 之间的数量关系并证明你的猜想.
相关试题

