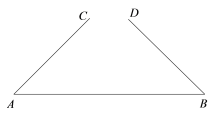
【题目】如图,线段![]() ,
,![]() ,
,![]() .点
.点![]() ,
,![]() 为线段
为线段![]() 上两点.从下面4个条件中:①
上两点.从下面4个条件中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .选择一个条件,使得
.选择一个条件,使得![]() 一定和
一定和![]() 全等 .则所有满足条件的序号是( )
全等 .则所有满足条件的序号是( )
A.①④B.②③C.①②④D.②③④
参考答案:
【答案】D
【解析】
利用全等三角形的判定定理对①②③④进行逐一判断即可.
解:①结合已知条件,判定条件为SSA.由于CE=5,AC=4![]() ,CE<AC,∴E点在线段AB上有两个符合条件的点,同理F也有两个符合条件的点,由图可知
,CE<AC,∴E点在线段AB上有两个符合条件的点,同理F也有两个符合条件的点,由图可知![]() 不一定和
不一定和![]() 全等,错误;
全等,错误;

②结合已知条件,由SAS可以判定![]() 和
和![]() 全等,正确;
全等,正确;
③由于CE=7,AC=4![]() , CE>AC,∴线段AB上只有一个符合条件的点E,同理只有一个符合条件的点F,如图,此时
, CE>AC,∴线段AB上只有一个符合条件的点E,同理只有一个符合条件的点F,如图,此时![]() 一定和
一定和![]() 全等.故正确;
全等.故正确;
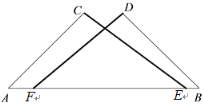
④∵![]() ,∴∠AEC=∠DFB,再结合已知条件,根据AAS,可以判定
,∴∠AEC=∠DFB,再结合已知条件,根据AAS,可以判定![]() 和
和![]() 全等.正确.
全等.正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.
●特例感知
①等腰直角三角形 勾股高三角形(请填写“是”或者“不是”);
②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若
 ,试求线段CD的长度.
,试求线段CD的长度.
●深入探究
如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;

●推广应用
如图3,等腰△ABC为勾股高三角形,其中
 ,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若
,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若 ,试求线段DE的长度.
,试求线段DE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在平面直角坐标系中,直线
 交坐标轴于A、B两点,过点C(
交坐标轴于A、B两点,过点C( ,0)作CD交AB于D,交
,0)作CD交AB于D,交 轴于点E.且△COE≌△BOA.
轴于点E.且△COE≌△BOA.
(1)求B点坐标为 ;线段OA的长为 ;
(2)确定直线CD解析式,求出点D坐标;
(3)如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.
①点M移动过程中,线段OM与ON数量关系是否不变,并证明;
②当△OMN面积最小时,求点M的坐标和△OMN面积.
-
科目: 来源: 题型:
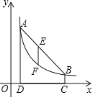
查看答案和解析>>【题目】如图,点
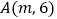 ,
,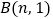 在反比例函数图象上,
在反比例函数图象上,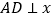 轴于点
轴于点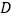 ,
,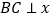 轴于点
轴于点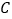 ,
,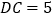 .
.
(1)求
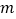 ,
,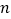 的值并写出反比例函数的表达式;
的值并写出反比例函数的表达式;(2)连接
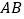 ,
,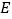 是线段
是线段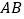 上一点,过点
上一点,过点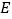 作
作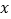 轴的垂线,交反比例函数图象于点
轴的垂线,交反比例函数图象于点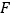 ,若
,若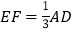 ,求出点
,求出点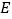 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
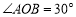 ,点
,点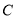 为射线
为射线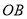 上一点,点
上一点,点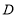 为
为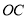 的中点,且
的中点,且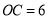 .当点
.当点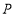 在射线
在射线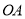 上运动时 ,则
上运动时 ,则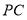 与
与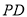 和的最小值为_______.
和的最小值为_______.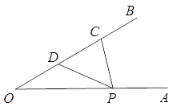
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 、
、 在反比例函数
在反比例函数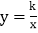 的图象上,且点
的图象上,且点 、
、 的横坐标分别为
的横坐标分别为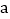 ,
,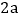
 .过点
.过点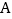 作
作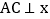 轴,垂足为
轴,垂足为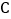 ,且
,且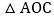 的面积为
的面积为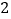 .
.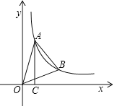
 求该反比例函数的解析式;
求该反比例函数的解析式; 若
若 ,设直线
,设直线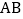 的解析式为
的解析式为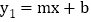 ,当
,当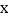 满足什么条件,
满足什么条件,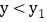 ?
?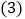 求
求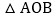 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形中,
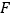 是
是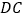 上的一点,直线
上的一点,直线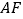 与
与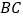 的延长线交于点
的延长线交于点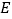 ,
, 并与
并与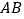 交于点
交于点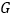 ,下列式子中错误的是( )
,下列式子中错误的是( )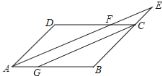
A.
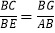 B.
B. 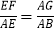 C.
C. 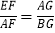 D.
D. 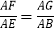
相关试题

