【题目】我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.
●特例感知
①等腰直角三角形 勾股高三角形(请填写“是”或者“不是”);
②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若![]() ,试求线段CD的长度.
,试求线段CD的长度.

●深入探究
如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;

●推广应用
如图3,等腰△ABC为勾股高三角形,其中![]() ,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若
,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若![]() ,试求线段DE的长度.
,试求线段DE的长度.

参考答案:
【答案】●特例感知:①是;②![]() ;
;
●深入探究: ![]() ,理由见解析;
,理由见解析;
●推广应用:2a.
【解析】试题分析:●特例感知
①根据勾股高三角形的定义进行判断即可.
②设![]() 根据勾股定理可得:
根据勾股定理可得: ![]() ,根据勾股高三角形的定义列出方程,解方程即可.
,根据勾股高三角形的定义列出方程,解方程即可.
●深入探究
根据勾股高三角形的定义结合勾股定理即可得出它们之间的关系.
●推广应用
运用探究的结果进行运算即可.
试题解析:
●特例感知
① 是 ;
②设![]()
根据勾股定理可得: ![]() ,
,
于是![]() ,
,
∴![]() ;
;
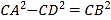
●深入探究
由![]() 可得:
可得: ![]() ,而
,而![]() ,
,
∴![]() ,即
,即![]() ;
;

●推广应用
过点A向ED引垂线,垂足为G,
∵“勾股高三角形”△ABC为等腰三角形,且![]() ,
,
∴只能是![]() ,由上问可知
,由上问可知![]() ……①.
……①.
又ED∥BC,∴![]() ……②.
……②.
而![]() ……③,
……③,
∴△AGD≌△CDB(AAS),于是![]() .
.
易知△ADE与△ABC均为等腰三角形,
根据三线合一原理可知![]() .
.
又![]() ∴
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,直线
 分别交
分别交 轴
轴 轴于
轴于 、
、 两点,
两点, 、
、 的长满足
的长满足 ,点
,点 是直线
是直线 上一点,且
上一点,且 .
.
 求直线
求直线 的解析式;
的解析式; 求过点
求过点 的反比例函数解析式;
的反比例函数解析式; 点
点 在反比例函数图象上是否存在一点
在反比例函数图象上是否存在一点 ,使以点
,使以点 、
、 、
、 、
、 为顶点,
为顶点, 为腰的四边形为梯形?若存在,请直接写出点
为腰的四边形为梯形?若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
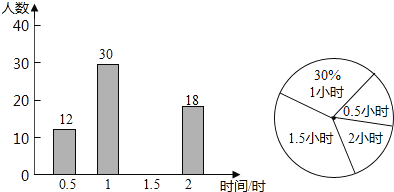
查看答案和解析>>【题目】为了提高学生阅读能力,我区某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;被调查的学生周末阅读时间众数是多少小时,中位数是多少小时;
(2)计算被调查学生阅读时间的平均数;
(3)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在平面直角坐标系中,直线
 交坐标轴于A、B两点,过点C(
交坐标轴于A、B两点,过点C( ,0)作CD交AB于D,交
,0)作CD交AB于D,交 轴于点E.且△COE≌△BOA.
轴于点E.且△COE≌△BOA.
(1)求B点坐标为 ;线段OA的长为 ;
(2)确定直线CD解析式,求出点D坐标;
(3)如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.
①点M移动过程中,线段OM与ON数量关系是否不变,并证明;
②当△OMN面积最小时,求点M的坐标和△OMN面积.
-
科目: 来源: 题型:
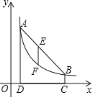
查看答案和解析>>【题目】如图,点
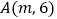 ,
,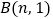 在反比例函数图象上,
在反比例函数图象上,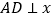 轴于点
轴于点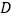 ,
,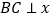 轴于点
轴于点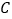 ,
,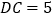 .
.
(1)求
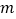 ,
,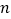 的值并写出反比例函数的表达式;
的值并写出反比例函数的表达式;(2)连接
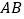 ,
,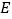 是线段
是线段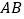 上一点,过点
上一点,过点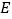 作
作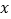 轴的垂线,交反比例函数图象于点
轴的垂线,交反比例函数图象于点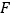 ,若
,若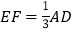 ,求出点
,求出点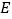 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段
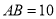 ,
,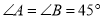 ,
,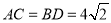 .点
.点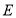 ,
,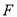 为线段
为线段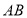 上两点.从下面4个条件中:①
上两点.从下面4个条件中:①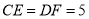 ;②
;②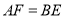 ;③
;③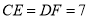 ;④
;④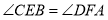 .选择一个条件,使得
.选择一个条件,使得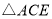 一定和
一定和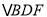 全等 .则所有满足条件的序号是( )
全等 .则所有满足条件的序号是( )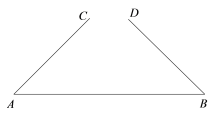
A.①④B.②③C.①②④D.②③④
相关试题

