【题目】如图,点![]() 、
、![]() 在反比例函数
在反比例函数![]() 的图象上,且点
的图象上,且点![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() ,
,![]()
![]() .过点
.过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,且
,且![]() 的面积为
的面积为![]() .
.
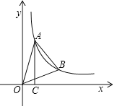
![]() 求该反比例函数的解析式;
求该反比例函数的解析式;
![]() 若
若![]() ,设直线
,设直线![]() 的解析式为
的解析式为![]() ,当
,当![]() 满足什么条件,
满足什么条件,![]() ?
?
![]() 求
求![]() 的面积.
的面积.
参考答案:
【答案】![]()
![]() ;
;![]() 当
当![]() 时,
时,![]() ;
;![]()
![]() .
.
【解析】
(1)根据反比例函数k的几何意义得到![]() ,即可得到k=4,于是得到反比例函数解析式为
,即可得到k=4,于是得到反比例函数解析式为![]() ;
;
(2)当a=5时,![]() ,
,![]() ,然后观察函数图象,找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可;
,然后观察函数图象,找出一次函数图象在反比例函数图象上方所对应的自变量的范围即可;
(3)过点B作BD⊥x轴,垂足为D,如图,根据反比例函数图象上点的坐标特征得![]() ,
,![]() ,由于S四边形AODB=S△AOC+S梯形ACDB=S△AOB+S△BOD,根据反比例函数k的几何意义得S△AOC=S△BOD,则S梯形ACDB=S△AOB,然后根据梯形公式计算即可.
,由于S四边形AODB=S△AOC+S梯形ACDB=S△AOB+S△BOD,根据反比例函数k的几何意义得S△AOC=S△BOD,则S梯形ACDB=S△AOB,然后根据梯形公式计算即可.
![]() ∵
∵![]() 轴,
轴,
∴![]() ,
,
即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴反比例函数解析式为![]() ;
;
![]() 当
当![]() 时,
时,![]() ,
,![]() ,
,
故当![]() 时,
时,![]() ;
;
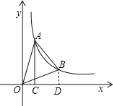
![]() 过点
过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,如图,
,如图,![]() ,
,![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]()
![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
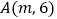 ,
,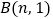 在反比例函数图象上,
在反比例函数图象上,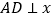 轴于点
轴于点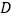 ,
,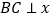 轴于点
轴于点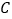 ,
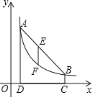
,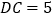 .
.
(1)求
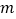 ,
,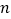 的值并写出反比例函数的表达式;
的值并写出反比例函数的表达式;(2)连接
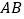 ,
,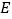 是线段
是线段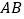 上一点,过点
上一点,过点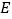 作
作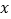 轴的垂线,交反比例函数图象于点
轴的垂线,交反比例函数图象于点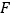 ,若
,若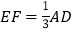 ,求出点
,求出点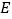 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段
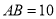 ,
,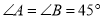 ,
,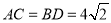 .点
.点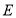 ,
,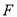 为线段
为线段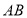 上两点.从下面4个条件中:①
上两点.从下面4个条件中:①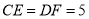 ;②
;②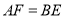 ;③
;③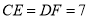 ;④
;④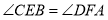 .选择一个条件,使得
.选择一个条件,使得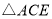 一定和
一定和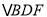 全等 .则所有满足条件的序号是( )
全等 .则所有满足条件的序号是( )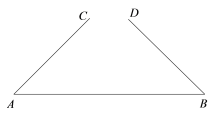
A.①④B.②③C.①②④D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
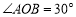 ,点
,点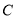 为射线
为射线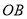 上一点,点
上一点,点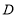 为
为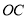 的中点,且
的中点,且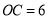 .当点
.当点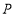 在射线
在射线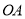 上运动时 ,则
上运动时 ,则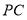 与
与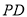 和的最小值为_______.
和的最小值为_______.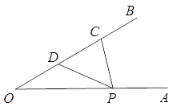
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形中,
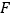 是
是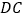 上的一点,直线
上的一点,直线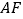 与
与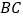 的延长线交于点
的延长线交于点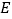 ,
, 并与
并与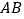 交于点
交于点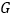 ,下列式子中错误的是( )
,下列式子中错误的是( )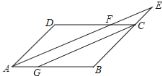
A.
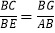 B.
B. 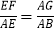 C.
C. 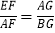 D.
D. 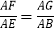
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是圆圆设计的“作等腰三角形一腰上的高线”的尺规作图过程 .
已知:△
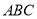 ,
,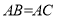 .
.求作:
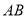 边上的高线.
边上的高线.作法:如图,

①以点
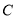 为圆心,
为圆心,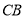 为半径画弧,交
为半径画弧,交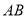 于点
于点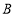 和点
和点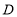 ;
;②分别以点
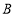 和点
和点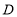 为圆心,大于
为圆心,大于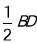 长为半径画弧,两弧相交于点
长为半径画弧,两弧相交于点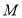 ;
;③作射线
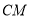 交
交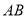 于点
于点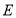 .
.所以线段
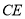 就是所求作的
就是所求作的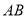 边上的高线.
边上的高线.根据圆圆设计的尺规作图过程,完成下列问题:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面证明.
证明:∵
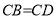 ,
,∴点
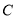 在线段
在线段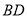 的垂直平分线上(__________) (填推理的依据).
的垂直平分线上(__________) (填推理的依据).∵__________=__________,
∴点
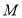 在线段
在线段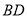 的垂直平分线上.
的垂直平分线上.∴
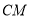 是线段
是线段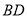 的垂直平分线.
的垂直平分线. ∴
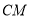 ⊥
⊥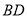 .
.∴线段
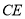 就是
就是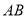 边上的高线.
边上的高线. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有
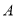 ,
, 两个不透明的袋子,分别装有3个除颜色外完全相同的小球,其中
两个不透明的袋子,分别装有3个除颜色外完全相同的小球,其中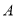 袋中装有2个白球,1个红球;
袋中装有2个白球,1个红球; 袋中装有2个红球,1个白球.小林和小华商定了一个游戏规则:从摇匀后的
袋中装有2个红球,1个白球.小林和小华商定了一个游戏规则:从摇匀后的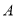 ,
, 两袋中各随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画树状图法,说明这个游戏对双方是否公平.
两袋中各随机摸出一个小球,摸出的这两个小球,若颜色相同,则小林获胜;若颜色不同,则小华获胜.请用列表法或画树状图法,说明这个游戏对双方是否公平.
相关试题

