【题目】如图,点![]() ,
,![]() 在反比例函数图象上,
在反比例函数图象上,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() .
.
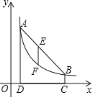
(1)求![]() ,
,![]() 的值并写出反比例函数的表达式;
的值并写出反比例函数的表达式;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,交反比例函数图象于点
轴的垂线,交反比例函数图象于点![]() ,若
,若![]() ,求出点
,求出点![]() 的坐标.
的坐标.
参考答案:
【答案】![]() ,
,![]() ,
,![]() ;
;![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)设反比例函数的解析式为![]() ,根据题意得出方程组
,根据题意得出方程组![]() ,求出方程组的解即可;
,求出方程组的解即可;
(2)设直线AB的解析式为y=ax+b,求出直线AB的解析式,设E点的横坐标为m,则![]() ,
,![]() ,求出
,求出![]() ,得出关于m的方程,求出m即可.
,得出关于m的方程,求出m即可.
![]() 设反比例函数的解析式为
设反比例函数的解析式为![]() ,
,
把![]() 代入得:
代入得:![]() ,
,
即![]() ,
,
∵点![]() ,
,![]() 在反比例函数图象上,
在反比例函数图象上,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
即![]() ,
,![]() ;
;
反比例函数的解析式为:![]() ;
;![]() 设直线
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 和
和![]() 代入得:
代入得:![]() ,
,
解得:![]() ,
,![]() ,
,
即直线![]() 的解析式为:
的解析式为:![]() ,
,
设![]() 点的横坐标为
点的横坐标为![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得:![]() ,
,![]() ,
,
经检验都是原方程的解,
即![]() 的坐标为
的坐标为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店11月份购进甲、乙两种水果共花费1700元,其中甲种水果8元/千克,乙种水果18元/千克.12月份,这两种水果的进价上调为:甲种水果10元/千克,乙种水果20元/千克.
(1)若该店12月份购进这两种水果的数量与11月份都相同,将多支付货款300元,求该店11月份购进甲、乙两种水果分别是多少千克?
(2)若12月份将这两种水果进货总量减少到120千克,设购进甲种水果a千克,需要支付的货款为w元,求w与a的函数关系式;
(3)在(2)的条件下,若甲种水果不超过90千克,则12月份该店需要支付这两种水果的货款最少应是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.
●特例感知
①等腰直角三角形 勾股高三角形(请填写“是”或者“不是”);
②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若
 ,试求线段CD的长度.
,试求线段CD的长度.
●深入探究
如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;

●推广应用
如图3,等腰△ABC为勾股高三角形,其中
 ,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若
,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若 ,试求线段DE的长度.
,试求线段DE的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在平面直角坐标系中,直线
 交坐标轴于A、B两点,过点C(
交坐标轴于A、B两点,过点C( ,0)作CD交AB于D,交
,0)作CD交AB于D,交 轴于点E.且△COE≌△BOA.
轴于点E.且△COE≌△BOA.
(1)求B点坐标为 ;线段OA的长为 ;
(2)确定直线CD解析式,求出点D坐标;
(3)如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.
①点M移动过程中,线段OM与ON数量关系是否不变,并证明;
②当△OMN面积最小时,求点M的坐标和△OMN面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,线段
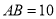 ,
,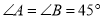 ,
,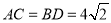 .点
.点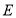 ,
,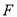 为线段
为线段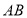 上两点.从下面4个条件中:①
上两点.从下面4个条件中:①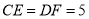 ;②
;②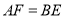 ;③
;③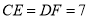 ;④
;④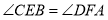 .选择一个条件,使得
.选择一个条件,使得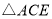 一定和
一定和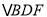 全等 .则所有满足条件的序号是( )
全等 .则所有满足条件的序号是( )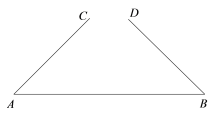
A.①④B.②③C.①②④D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
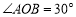 ,点
,点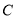 为射线
为射线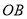 上一点,点
上一点,点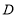 为
为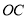 的中点,且
的中点,且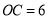 .当点
.当点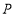 在射线
在射线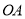 上运动时 ,则
上运动时 ,则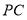 与
与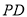 和的最小值为_______.
和的最小值为_______.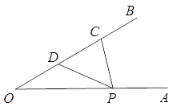
-
科目: 来源: 题型:
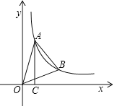
查看答案和解析>>【题目】如图,点
 、
、 在反比例函数
在反比例函数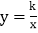 的图象上,且点
的图象上,且点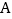 、
、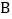 的横坐标分别为
的横坐标分别为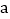 ,
,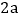
 .过点
.过点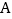 作
作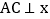 轴,垂足为
轴,垂足为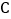 ,且
,且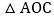 的面积为
的面积为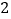 .
.
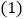 求该反比例函数的解析式;
求该反比例函数的解析式;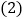 若
若 ,设直线
,设直线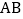 的解析式为
的解析式为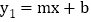 ,当
,当 满足什么条件,
满足什么条件,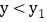 ?
?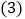 求
求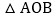 的面积.
的面积.
相关试题

