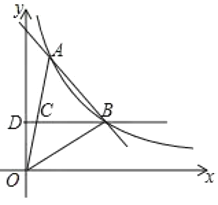
【题目】如图,一次函数y=ax+b与反比例函数y=![]() (x>0)的图像在第一象限交于A、B两点,点B坐标为(4,2),连接OA、OB,过点B作BD⊥y轴,垂足为D,交OA于点C,且OC=CA.
(x>0)的图像在第一象限交于A、B两点,点B坐标为(4,2),连接OA、OB,过点B作BD⊥y轴,垂足为D,交OA于点C,且OC=CA.
(1)求反比例函数和一次函数的表达式;
(2)根据图像直接说出不等式ax+b-![]() <0的解集为______;
<0的解集为______;
(3)求△ABC的面积.
参考答案:
【答案】(1)y=-x+6;y=![]() ;(2)0<x<2或x>4;(3)S△ABC=3.
;(2)0<x<2或x>4;(3)S△ABC=3.
【解析】
(1)此处由题意可先求出反比例函数表达式,再根据CO=CA设出A点坐标求出A点坐标,代入即可求出一次函数表达式.
(2)此处根据数形结合找出一次函数与反比例函数关系即可.
(3)此题可先求出C点坐标,根据A,B,C三点坐标求面积即可.
(1)如图,过点A作AF⊥x轴交BD于E,
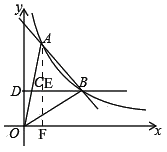
∵点B(4,2)在反比例函数y=![]() 的图象上,
的图象上,
∴k=4×2=8,
∴反比例函数的表达式为y=![]() ,
,
∵B(4,2),
∴EF=2,
∵BD⊥y轴,OC=CA,
∴AE=EF=![]() AF,
AF,
∴AF=4,
∴点A的纵坐标为4,
∵点A在反比例函数y=![]() 的图象上,
的图象上,
∴A(2,4),
∴4a+b=2;2a+b=4,
∴a=-1 b=6,
∴一次函数的表达式为y=-x+6;
(2)0<x<2或x>4.
(3)如图1,过点A作AF⊥x轴于F交OB于G,
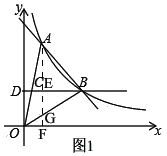
∵A(2,4),
∴直线OA的解析式为y=2x,
∴C(1,2),
∵A(2,4),
∴AE=4-2=2,BC=4-1=3,
∴S△ABC=![]() ×2×3=3.
×2×3=3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C三点分别在反比例函数y=
 (x<0)、y=
(x<0)、y= (x>0)、y=
(x>0)、y= (x>0)的图象上,AC⊥y轴于点E,BC⊥x轴于点F,AB经过原点,若S△ABC=5,则k1+k2-2k3的值为________.
(x>0)的图象上,AC⊥y轴于点E,BC⊥x轴于点F,AB经过原点,若S△ABC=5,则k1+k2-2k3的值为________.
-
科目: 来源: 题型:
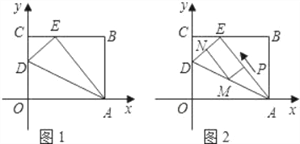
查看答案和解析>>【题目】如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标;
(2)如图2,若AE上有一动点P(不与A,E重合)自A点沿AE方向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,s有最大值,最大值是多少?
(3)在(2)的条件下,当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠MON=90°,点A、B分别在OM、ON上运动(不与点O重合).
(1)如图①,BC是∠ABN的平分线,BC的反方向延长线与∠BAO的平分线交于点D.
①若∠BAO=60°,则∠D的大小为 度,
②猜想:∠D的度数是否随A、B的移动发生变化?请说明理由.
(2)如图②,若∠ABC=
 ∠ABN, ∠BAD=
∠ABN, ∠BAD= ∠BAO,则∠D的大小为 度,若∠ABC=
∠BAO,则∠D的大小为 度,若∠ABC=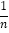 ∠ABN, ∠BAD=
∠ABN, ∠BAD=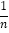 ∠BAO,则∠D的大小为 度(用含n的代数式表示).
∠BAO,则∠D的大小为 度(用含n的代数式表示).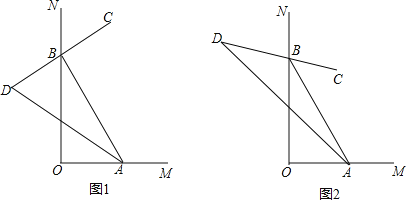
-
科目: 来源: 题型:
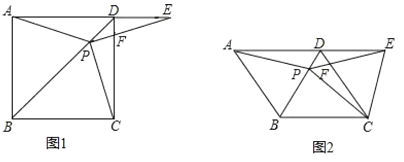
查看答案和解析>>【题目】如图①,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PC=PE,PE交CD于点F.
(1)求证:∠PCD=∠PED;
(2)连接EC,求证:EC=
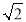 AP;
AP;(3)如图②,把正方形ABCD改成菱形ABCD,其他条件不变,当∠DAB=60°时,请直接写出线段EC和AP的数量关系______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一张三角形纸片ABC,∠A=80°,∠B=70°,D是AC边上一定点,过点D将纸片的一角折叠,使点C落在BC下方C′处,折痕DE与BC交于点E,当AB与∠C′的一边平行时,∠DEC'=_____度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:己知:对于实数a≥0,b≥0,满足a+b≥2
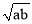 ,当且仅当a = b时,等号成立,此时取得代数式a+b的最小值.
,当且仅当a = b时,等号成立,此时取得代数式a+b的最小值.根据以上结论,解决以下问题:
(1)拓展:若a>0,当且仅当a=___时,a+
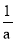 有最小值,最小值为____;
有最小值,最小值为____;(2)应用:
①如图1,已知点P为双曲线y=
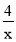 (x>0)上的任意一点,过点P作PA⊥x轴,PB丄y轴,四边形OAPB的周长取得最小值时,求出点P的坐标以及周长最小值:
(x>0)上的任意一点,过点P作PA⊥x轴,PB丄y轴,四边形OAPB的周长取得最小值时,求出点P的坐标以及周长最小值:②如图2,已知点Q是双曲线y=
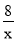 (x>0)上一点,且PQ∥x轴, 连接OP、OQ,当线段OP取得最小值时,在平面内取一点C,使得以0、P、Q、C为顶点的四边形是平行四边形,求出点C的坐标.
(x>0)上一点,且PQ∥x轴, 连接OP、OQ,当线段OP取得最小值时,在平面内取一点C,使得以0、P、Q、C为顶点的四边形是平行四边形,求出点C的坐标.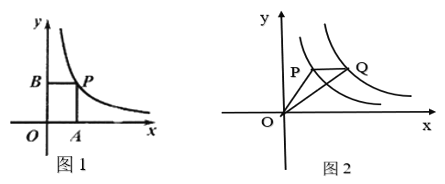
相关试题

