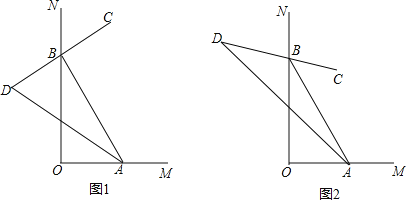
【题目】如图,∠MON=90°,点A、B分别在OM、ON上运动(不与点O重合).
(1)如图①,BC是∠ABN的平分线,BC的反方向延长线与∠BAO的平分线交于点D.
①若∠BAO=60°,则∠D的大小为 度,
②猜想:∠D的度数是否随A、B的移动发生变化?请说明理由.
(2)如图②,若∠ABC=![]() ∠ABN, ∠BAD=
∠ABN, ∠BAD=![]() ∠BAO,则∠D的大小为 度,若∠ABC=
∠BAO,则∠D的大小为 度,若∠ABC=![]() ∠ABN, ∠BAD=
∠ABN, ∠BAD=![]() ∠BAO,则∠D的大小为 度(用含n的代数式表示).
∠BAO,则∠D的大小为 度(用含n的代数式表示).
参考答案:
【答案】(1)① 45,②否,理由见解析;(2)30°,![]() .
.
【解析】
(1)①先求出∠ABN=150°,再根据角平分线得出∠CBA=![]() ∠ABN=75°、∠BAD=
∠ABN=75°、∠BAD=![]() ∠BAO=30°,最后由外角性质可得∠D度数;
∠BAO=30°,最后由外角性质可得∠D度数;
②设∠BAD=α,利用外角性质和角平分线性质求得∠ABC=45°+α,利用∠D=∠ABC-∠BAD可得答案;
(2)设∠BAD=α,得∠BAO=3α,继而求得∠ABN=90°+3α、∠ABC=30°+α,根据∠D=∠ABC-∠BAD可得答案;设∠BAD=β,分别求得∠BAO=nβ、∠ABN=∠AOB+∠BAO=90+nβ、∠ABC=![]() +β,由∠D=∠ABC-∠BAD得出答案.
+β,由∠D=∠ABC-∠BAD得出答案.
(1)①∵∠BAO=60°、∠MON=90°,
∴∠ABN=150°,
∵BC平分∠ABN、AD平分∠BAO,
∴∠CBA=![]() ∠ABN=75°,∠BAD=
∠ABN=75°,∠BAD=![]() ∠BAO=30°,
∠BAO=30°,
∴∠D=∠CBA-∠BAD=45°,
故答案为:45;
②∠D的度数不变.
理由:设∠BAD=α.
∵AD平分∠BAO,
∴∠BAO=2α.
∵∠ABN=∠AOB+∠BAO,
∴∠ABN =90°+2α.
∵BC平分∠ABN,
∴∠ABC=![]() ∠ABN=
∠ABN=![]() (90°+2α) =45°+α.
(90°+2α) =45°+α.
∵∠D=∠ABC-∠BAD,
∴∠D =45°+α-α=45°.
(2)设∠BAD=α,
∵∠BAD=![]() ∠BAO,
∠BAO,
∴∠BAO=3α,
∵∠AOB=90°,
∴∠ABN=∠AOB+∠BAO=90°+3α,
∵∠ABC=![]() ∠ABN,
∠ABN,
∴∠ABC=30°+α,
∴∠D=∠ABC-∠BAD=30°+α-α=30°,
设∠BAD=β,
∵∠BAD=![]() ∠BAO,
∠BAO,
∴∠BAO=nβ,
∵∠AOB=90°,
∴∠ABN=∠AOB+∠BAO=90°+nβ,
∵∠ABC=![]() ∠ABN,
∠ABN,
∴∠ABC=![]() +β,
+β,
∴∠D=∠ABC-∠BAD=![]() +β-β=
+β-β=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为提高市民的环保意识,倡导“节能减排,绿色出行”,某市计划在城区投放一批“共享单车”,这批单车分为A、B两种不同款型,其中A型车单价400元,B型车单价320元.
(1)今年年初,“共享单车”试点投放在某市中心城区正式启动,投放A、B两种款型的单车共100辆,总价值36800元.求本次试点投放的A型车、B型车的辆数.
(2)试点投放活动得到了广大市民的认可,该市决定将此项公益活动在整个城区全面铺开.按照试点投放中A、B两车型的数量比进行投放,且投资总价值不低于184万元.问整个城区全面铺开时投放的A型车、B型车至少多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C三点分别在反比例函数y=
 (x<0)、y=
(x<0)、y= (x>0)、y=
(x>0)、y= (x>0)的图象上,AC⊥y轴于点E,BC⊥x轴于点F,AB经过原点,若S△ABC=5,则k1+k2-2k3的值为________.
(x>0)的图象上,AC⊥y轴于点E,BC⊥x轴于点F,AB经过原点,若S△ABC=5,则k1+k2-2k3的值为________.
-
科目: 来源: 题型:
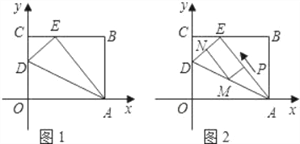
查看答案和解析>>【题目】如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标;
(2)如图2,若AE上有一动点P(不与A,E重合)自A点沿AE方向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,s有最大值,最大值是多少?
(3)在(2)的条件下,当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标?
-
科目: 来源: 题型:
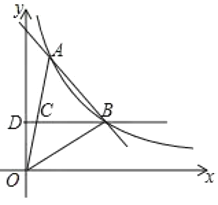
查看答案和解析>>【题目】如图,一次函数y=ax+b与反比例函数y=
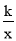 (x>0)的图像在第一象限交于A、B两点,点B坐标为(4,2),连接OA、OB,过点B作BD⊥y轴,垂足为D,交OA于点C,且OC=CA.
(x>0)的图像在第一象限交于A、B两点,点B坐标为(4,2),连接OA、OB,过点B作BD⊥y轴,垂足为D,交OA于点C,且OC=CA.(1)求反比例函数和一次函数的表达式;
(2)根据图像直接说出不等式ax+b-
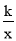 <0的解集为______;
<0的解集为______;(3)求△ABC的面积.
-
科目: 来源: 题型:
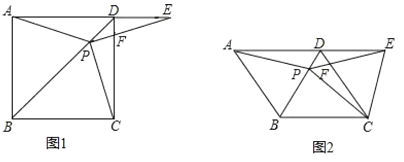
查看答案和解析>>【题目】如图①,在正方形ABCD中,点P是对角线BD上的一点,点E在AD的延长线上,且PC=PE,PE交CD于点F.
(1)求证:∠PCD=∠PED;
(2)连接EC,求证:EC=
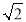 AP;
AP;(3)如图②,把正方形ABCD改成菱形ABCD,其他条件不变,当∠DAB=60°时,请直接写出线段EC和AP的数量关系______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一张三角形纸片ABC,∠A=80°,∠B=70°,D是AC边上一定点,过点D将纸片的一角折叠,使点C落在BC下方C′处,折痕DE与BC交于点E,当AB与∠C′的一边平行时,∠DEC'=_____度.

相关试题

