【题目】如图1,在平面直角坐标系中,A、B,C三点的坐标分别为(0,1)、(3,3)、(4,0).
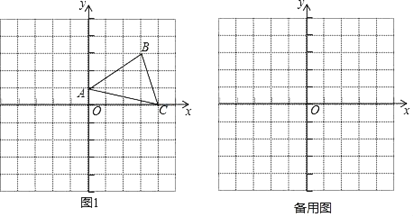
(I)S△AOC= ;
(2)若点P(m﹣1,1)是第二象限内一点,且△AOP的面积不大于△ABC的面积,求m的取值范围;
(3)若将线段AB向左平移1个单位长度,点D为x轴上一点,点E(4,n)为第一象限内一动点,连BE、CE、AC,若△ABD的面积等于由AB、BE、CE、AC四条线段围成图形的面积,则点D的坐标为 .(用含n的式子表示)
参考答案:
【答案】(1)2;(2)﹣10≤m<1;(3)(![]() +4,0)或(﹣
+4,0)或(﹣![]() ﹣9,0)
﹣9,0)
【解析】
(1)求出OA、OC即可解决问题;
(2)求出△ABC的面积,根据不等式即可解决问题;
(3)如图2中,延长BA交x轴于K,连接BC.首先求出直线AB的解析式,可得点K坐标,根据S△ABD=S四边形ABEC,可得S△BKD﹣S△AKD=S△BCK+S△BCE﹣S△ACK,由此构建方程即可解决问题;
解:(1)∵A(0,1),C(4,0),
∴OA=1,OC=4,
∴![]()
故答案为2.
(2)如图1,作BH⊥y轴于H.
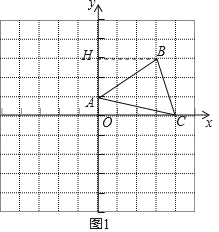
S△ABC=S四边形OCBH﹣S△ABH﹣S△OAC
![]()
![]()
由题意, ![]()
∴m≥﹣10,
∵P在第二象限,
∴m﹣1<0,
∴m<1,
∴﹣10≤m<1.
(3)如图2中,延长BA交x轴于K,连接BC.
∵A(﹣1,1),B(2,3),
设直线AB的解析式为y=kx+b,则有![]()
解得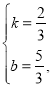
∴直线AB的解析式为![]()
∴![]() 当点D在K的右边,设D(m,0),
当点D在K的右边,设D(m,0),
∵S△ABD=S四边形ABEC,
∴S△BKD﹣S△AKD=S△BCK+S△BCE﹣S△ACK,
∴![]()
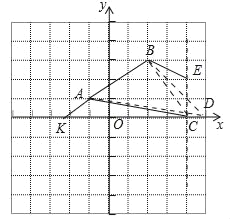
解得![]()
∴![]()
根据对称性可知,当点D′在K的左侧时,D′K=DK,可得![]()
综上所述,满足条件的D的坐标![]() 或
或![]()
方法二:当点D在K的右边,设D(m,0),(m>4),
∵![]()
S四边形ABEC=S△ABC+S△BCE![]()
![]() 解得
解得![]() 接下来同上面.
接下来同上面.
故答案为:![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线L:y=﹣
 (x+t)(x﹣t+4)与x轴只有一个交点,则抛物线L与x轴的交点坐标是 .
(x+t)(x﹣t+4)与x轴只有一个交点,则抛物线L与x轴的交点坐标是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+2x+k+2与x轴的公共点有两个.
(1)求k的取值范围;
(2)当k=1时,求抛物线与x轴的公共点A和B的坐标及顶点C的坐标;
(3)观察图象,当x取何值时y>0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点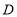 、
、 分别是边
分别是边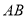 、
、 的中点,延长
的中点,延长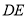 至
至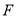 ,使得
,使得 ,连接
,连接 、
、 .
.
(1)求证:四边形
 是菱形;
是菱形;(2)当
 ,
, 时,判断
时,判断 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 与
与 轴交于点
轴交于点 ,与直线
,与直线 相交于点
相交于点 ,直线
,直线 与
与 轴正半轴、
轴正半轴、 轴围成的
轴围成的 的面积为
的面积为 .
.(1)求直线
 的解析式;
的解析式;(2)求点
 坐标并判断
坐标并判断 的形状,说明理由;
的形状,说明理由;(3)在
 轴上找一点
轴上找一点 ,使
,使 的面积为
的面积为 ,求
,求 点坐标.
点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】通程电器商城购
 台空调、
台空调、 台彩电需花费
台彩电需花费 万元.购
万元.购 台空调、
台空调、 台彩电需花费
台彩电需花费 万元.
万元.(1)计算每台空调与彩电的进价分别是多少元?
(2)已知一次性购进空调、彩电共
 台,购进资金不超过
台,购进资金不超过 万元,购进空调不少于
万元,购进空调不少于 台,写出符合要求的进货方案;
台,写出符合要求的进货方案;(3)在(2)的情况下,原每台空调的售价为
 元.每台彩电的售价为
元.每台彩电的售价为 元,根据市场需要,商城举行“庆五一优惠活动”,每台空调让利
元,根据市场需要,商城举行“庆五一优惠活动”,每台空调让利 元
元 .设商城计划购进空调
.设商城计划购进空调 台,空调和彩电全部销售完商城获得的利润为
台,空调和彩电全部销售完商城获得的利润为 元.试写出
元.试写出 与
与 的函数关系式,选择哪种进货方案,商城获利最大?
的函数关系式,选择哪种进货方案,商城获利最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0,其中k为常数.
(1)求证:无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
相关试题

