【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 的中点,延长
的中点,延长![]() 至
至![]() ,使得
,使得![]() ,连接
,连接![]() 、
、![]() .
.

(1)求证:四边形![]() 是菱形;
是菱形;
(2)当![]() ,
,![]() 时,判断
时,判断![]() 的形状,并说明理由.
的形状,并说明理由.
参考答案:
【答案】(1)详见解析;(2)![]() 是底角为
是底角为![]() 的等腰三角形,解析解析
的等腰三角形,解析解析
【解析】
(1)由“ASA“可证△AEF≌△CED,可得AF=CD,根据邻边相等的平行四边形是菱形即可证明;
(2)由勾股定理可求AB的长,由中位线定理可求DF=DB=5,即可求解.
(1)∵AF∥CD,
∴∠EAF=∠ECD,
∵E是AC中点,
∴AE=EC,
在△AEF和△CED中,
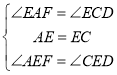
∴△AEF≌△CED(ASA),
∴AF=CD,
∴四边形AFCD是平行四边形,
∵∠ACB=![]() ,AD=DB,
,AD=DB,
∴CD=AD=BD,
∴四边形AFCD是菱形.
(2)∵∠ACB=![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
∴AB=![]()
∵点D,E分别是边AB,AC的中点,
∴BC=2DE,DB=![]() AB=5,
AB=5,
∵四边形AFCD是菱形,
∴DF=2DE=BC=5,
∴DF=DB,
∴△DFB是等腰三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+3与x轴的两个交点分别为(m,0)和(n,0),则当x=m+n时,y的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线L:y=﹣
 (x+t)(x﹣t+4)与x轴只有一个交点,则抛物线L与x轴的交点坐标是 .
(x+t)(x﹣t+4)与x轴只有一个交点,则抛物线L与x轴的交点坐标是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+2x+k+2与x轴的公共点有两个.
(1)求k的取值范围;
(2)当k=1时,求抛物线与x轴的公共点A和B的坐标及顶点C的坐标;
(3)观察图象,当x取何值时y>0. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A、B,C三点的坐标分别为(0,1)、(3,3)、(4,0).
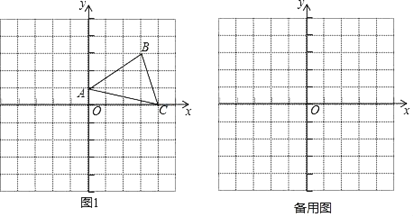
(I)S△AOC= ;
(2)若点P(m﹣1,1)是第二象限内一点,且△AOP的面积不大于△ABC的面积,求m的取值范围;
(3)若将线段AB向左平移1个单位长度,点D为x轴上一点,点E(4,n)为第一象限内一动点,连BE、CE、AC,若△ABD的面积等于由AB、BE、CE、AC四条线段围成图形的面积,则点D的坐标为 .(用含n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 与
与 轴交于点
轴交于点 ,与直线
,与直线 相交于点
相交于点 ,直线
,直线 与
与 轴正半轴、
轴正半轴、 轴围成的
轴围成的 的面积为
的面积为 .
.(1)求直线
 的解析式;
的解析式;(2)求点
 坐标并判断
坐标并判断 的形状,说明理由;
的形状,说明理由;(3)在
 轴上找一点
轴上找一点 ,使
,使 的面积为
的面积为 ,求
,求 点坐标.
点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】通程电器商城购
 台空调、
台空调、 台彩电需花费
台彩电需花费 万元.购
万元.购 台空调、
台空调、 台彩电需花费
台彩电需花费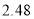 万元.
万元.(1)计算每台空调与彩电的进价分别是多少元?
(2)已知一次性购进空调、彩电共
 台,购进资金不超过
台,购进资金不超过 万元,购进空调不少于
万元,购进空调不少于 台,写出符合要求的进货方案;
台,写出符合要求的进货方案;(3)在(2)的情况下,原每台空调的售价为
 元.每台彩电的售价为
元.每台彩电的售价为 元,根据市场需要,商城举行“庆五一优惠活动”,每台空调让利
元,根据市场需要,商城举行“庆五一优惠活动”,每台空调让利 元
元 .设商城计划购进空调
.设商城计划购进空调 台,空调和彩电全部销售完商城获得的利润为
台,空调和彩电全部销售完商城获得的利润为 元.试写出
元.试写出 与
与 的函数关系式,选择哪种进货方案,商城获利最大?
的函数关系式,选择哪种进货方案,商城获利最大?
相关试题

