【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0,其中k为常数.
(1)求证:无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
参考答案:
【答案】
(1)证明:∵△=(k﹣5)2﹣4(1﹣k)=k2﹣6k+21=(k﹣3)2+12>0,
∴无论k为何值,方程总有两个不相等实数根
(2)解:∵二次函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,
∵二次项系数a=1,
∴抛物线开口方向向上,
∵△=(k﹣3)2+12>0,
∴抛物线与x轴有两个交点,
设抛物线与x轴的交点的横坐标分别为x1 , x2 ,
∴x1+x2=5﹣k>0,x1x2=1﹣k≥0,
解得k≤1,
即k的取值范围是k≤1
(3)解:设方程的两个根分别是x1 , x2 ,
根据题意,得(x1﹣3)(x2﹣3)<0,
即x1x2﹣3(x1+x2)+9<0,
又x1+x2=5﹣k,x1x2=1﹣k,
代入得,1﹣k﹣3(5﹣k)+9<0,
解得k< ![]() .
.
则k的最大整数值为2
【解析】 (1)先计算b2-4ac,再将b2-4ac的值转化为一个的代数式的平方加上一个正数,即可证出结论。
(2)根据此抛物线的图像不经过第三象限,而抛物线与x轴必有两个交点,可知抛物线的顶点在x轴的下方(第四象限)且图像经过第一、二、四象限,根据二次项的系数可知抛物线开口向上,设抛物线与x轴的交点的横坐标分别为x1 , x2 , 根据x1+x2>0,x1x2≥0,建立关于k的不等式组,求解即可。
(3)设方程的两个根分别是x1 , x2 , 根据已知原方程的一个根大于3,另一个根小于3,建立不等式(x1﹣3)(x2﹣3)<0,,再将不等式转化为含有x1x2和x1+x2的式子,再利用根与系数的关系,建立关于k的不等式,求解即可。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A、B,C三点的坐标分别为(0,1)、(3,3)、(4,0).
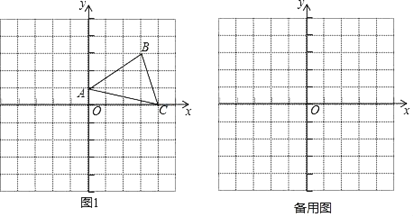
(I)S△AOC= ;
(2)若点P(m﹣1,1)是第二象限内一点,且△AOP的面积不大于△ABC的面积,求m的取值范围;
(3)若将线段AB向左平移1个单位长度,点D为x轴上一点,点E(4,n)为第一象限内一动点,连BE、CE、AC,若△ABD的面积等于由AB、BE、CE、AC四条线段围成图形的面积,则点D的坐标为 .(用含n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 与
与 轴交于点
轴交于点 ,与直线
,与直线 相交于点
相交于点 ,直线
,直线 与
与 轴正半轴、
轴正半轴、 轴围成的
轴围成的 的面积为
的面积为 .
.(1)求直线
 的解析式;
的解析式;(2)求点
 坐标并判断
坐标并判断 的形状,说明理由;
的形状,说明理由;(3)在
 轴上找一点
轴上找一点 ,使
,使 的面积为
的面积为 ,求
,求 点坐标.
点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】通程电器商城购
 台空调、
台空调、 台彩电需花费
台彩电需花费 万元.购
万元.购 台空调、
台空调、 台彩电需花费
台彩电需花费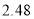 万元.
万元.(1)计算每台空调与彩电的进价分别是多少元?
(2)已知一次性购进空调、彩电共
 台,购进资金不超过
台,购进资金不超过 万元,购进空调不少于
万元,购进空调不少于 台,写出符合要求的进货方案;
台,写出符合要求的进货方案;(3)在(2)的情况下,原每台空调的售价为
 元.每台彩电的售价为
元.每台彩电的售价为 元,根据市场需要,商城举行“庆五一优惠活动”,每台空调让利
元,根据市场需要,商城举行“庆五一优惠活动”,每台空调让利 元
元 .设商城计划购进空调
.设商城计划购进空调 台,空调和彩电全部销售完商城获得的利润为
台,空调和彩电全部销售完商城获得的利润为 元.试写出
元.试写出 与
与 的函数关系式,选择哪种进货方案,商城获利最大?
的函数关系式,选择哪种进货方案,商城获利最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°.其中正确的结论是( )
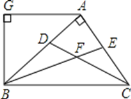
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】山东全省2016年国庆假期旅游人数增长12.5%,其中尤其是乡村旅游最为火爆.泰山脚下的某旅游村,为接待游客住宿需要,开设了有100张床位的旅馆,当每张床位每天收费100元时,床位可全部租出,若每张床位每天收费提高20元,则相应的减少了10张床位租出,如果每张床位每天以20元为单位提高收费,为使租出的床位少且租金高,那么每张床位每天最合适的收费是( )
A.140元
B.150元
C.160元
D.180元 -
科目: 来源: 题型:
查看答案和解析>>【题目】请把以下证明过程补充完整:
已知:如图,∠A=∠F,∠C=∠D.点B,E分别在线段AC,DF上,对∠1=∠2进行说理.

理由:∵∠A=∠F(已知)
∴______∥FD (______)
∴∠D=______(两直线平行,内错角相等)
∵∠C=∠D(已知)
∴______=∠C(等量代换)
∴______∥______(同位角相等,两直线平行)
∴∠1=∠3(______)
∵∠2=∠3(______)
∴∠1=∠2(等量代换).
相关试题

