【题目】已知二次函数y=﹣x2+2x+k+2与x轴的公共点有两个.
(1)求k的取值范围;
(2)当k=1时,求抛物线与x轴的公共点A和B的坐标及顶点C的坐标;
(3)观察图象,当x取何值时y>0.
参考答案:
【答案】
(1)解:∵二次函数y=﹣x2+2x+k+2与x轴有两个交点.
∴△=22﹣4×(﹣1)×(k+2)>0
解得:k>﹣3;
(2)解:当k=1时,二次函数是y=﹣x2+2x+3,
令y=0,得﹣x 2+2x+3=0,
解得:x 1=﹣1,x 2=3
∴抛物线与X轴的公共点A、B的坐标分别是(﹣1,0)、(3,0),
∵y=﹣x 2+2x+3=﹣(x﹣1)2+4
∴抛物线的顶点C的坐标是(1,4)
(3)解:由图象可知:当x=﹣1或x=3时,y=0;
当﹣1<x<3时,y>0.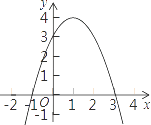
【解析】(1)抓住已知二次函数与x轴有两个交点得出b2-4ac>0,列不等式求出解集即可。
(2)将k=1代入函数解析式求出二次函数解析式,再根据y=0,解关于x的一元二次方程,求出x的值,就可得出抛物线与X轴的公共点A、B的坐标;然后将二次函数解析式配方成y=a(x-h)2+k的形式,就可求出其顶点坐标。
(3)先根据顶点坐标,抛物线与x轴的交点坐标、抛物线与y轴的交点坐标画出函数图像,再观察图像y>0,即是观察x轴上方的图像,就可写出自变量的取值范围。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(﹣1,0)与点C(x2 , 0),且与y轴交于点B(0,﹣2),小强得到以下结论:①0<a<2;②﹣1<b<0;③c=﹣1;④当|a|=|b|时x2>
 ﹣1;以上结论中正确结论的序号为 .
﹣1;以上结论中正确结论的序号为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+3与x轴的两个交点分别为(m,0)和(n,0),则当x=m+n时,y的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线L:y=﹣
 (x+t)(x﹣t+4)与x轴只有一个交点,则抛物线L与x轴的交点坐标是 .
(x+t)(x﹣t+4)与x轴只有一个交点,则抛物线L与x轴的交点坐标是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,点
,点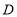 、
、 分别是边
分别是边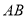 、
、 的中点,延长
的中点,延长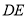 至
至 ,使得
,使得 ,连接
,连接 、
、 .
.
(1)求证:四边形
 是菱形;
是菱形;(2)当
 ,
, 时,判断
时,判断 的形状,并说明理由.
的形状,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,A、B,C三点的坐标分别为(0,1)、(3,3)、(4,0).
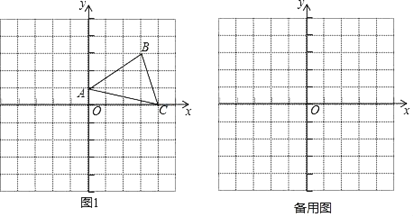
(I)S△AOC= ;
(2)若点P(m﹣1,1)是第二象限内一点,且△AOP的面积不大于△ABC的面积,求m的取值范围;
(3)若将线段AB向左平移1个单位长度,点D为x轴上一点,点E(4,n)为第一象限内一动点,连BE、CE、AC,若△ABD的面积等于由AB、BE、CE、AC四条线段围成图形的面积,则点D的坐标为 .(用含n的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 与
与 轴交于点
轴交于点 ,与直线
,与直线 相交于点
相交于点 ,直线
,直线 与
与 轴正半轴、
轴正半轴、 轴围成的
轴围成的 的面积为
的面积为 .
.(1)求直线
 的解析式;
的解析式;(2)求点
 坐标并判断
坐标并判断 的形状,说明理由;
的形状,说明理由;(3)在
 轴上找一点
轴上找一点 ,使
,使 的面积为
的面积为 ,求
,求 点坐标.
点坐标.
相关试题

