【题目】如图,在△ABC中,AC=BC,D是BC上的一点,且满足∠BAD= ![]() ∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
(1)求证:直线BC是⊙O的切线;
(2)连接EF,若tan∠AEF= ![]() ,AD=4,求BD的长.
,AD=4,求BD的长.
参考答案:
【答案】
(1)证明:在△ABC中,
∵AC=BC,
∴∠CAB=∠B,
∵∠CAB+∠B+∠C=180°,
∴2∠B+∠C=180°,
∴∠B+ ![]() ∠C=90°,
∠C=90°,
∵∠BAD= ![]() ∠C,
∠C,
∴∠B+∠BAD=90°,
∴∠ADB=90°,
∴AD⊥BC,
∵AD为⊙O直径,
∴直线BC是⊙O的切线;
(2)解:如图,连接DF,EF.
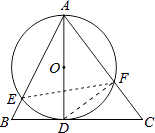
∵AD是⊙O的直径,
∴∠AFD=90°,
∵∠ADC=90°,
∴∠ADF+∠FDC=∠C+∠FDC=90°,
∴∠ADF=∠C,
∵∠ADF=∠AEF,tan∠AEF= ![]() ,
,
∴tan∠C=tan∠ADF= ![]() ,
,
在Rt△ACD中,设AD=4x,则CD=3x,
∴AC= ![]() =5x,
=5x,
∴BC=5x,BD=2x,
∵AD=4,
∴x=1,
∴BD=2.
【解析】(1)首先依据等腰三角形的性质得到∠CAB=∠B,然后结合三角形的内角和定理可得到∠B+ 1 2 ∠C=90°,然后依据题目条件可证明∠B+∠BAD=90°,然后依据切线的判定定理进行证明即可;
(2)连接DF,EF,由圆周角定理可知DF⊥AC,然后依据同角的余角相等得到∠ADF=∠C,接下来,依据同弧所对的圆周角相等得到∠ADF=∠AEF,由tan∠AEF的值得到tan∠ADF的值,设出AD=4x、DC=3x,再由AC=BC,根据BC-CD表示出BD,再由AD的长,最后,利用勾股定理求出x的值,从而可确定出BD的长.
【考点精析】根据题目的已知条件,利用勾股定理的概念和切线的判定定理的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学知识伴随着人类文明的起源而产生,人类祖先为我们留下了许多珍贵的原始资料,古巴比伦楔形文字泥板书就是其中之一,古巴比伦泥板上记载了两种利用平方数表计算两数乘积的公式:
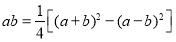 …①
…①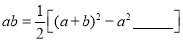 …②
…②(1)材料中,公式②中的空缺部分应该是 ;
(2)请你验证材料中的公式①;
(3)当
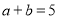 ,
, 时,利用公式①计算
时,利用公式①计算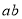 的值为 .
的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=
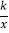 (k为常数,k≠0)的图象交于A、B两点,过点A作AC⊥x轴,垂足为C,连接OA,已知OC=2,tan∠AOC=
(k为常数,k≠0)的图象交于A、B两点,过点A作AC⊥x轴,垂足为C,连接OA,已知OC=2,tan∠AOC= ,B(m,﹣2)
,B(m,﹣2)(1)求一次函数和反比例函数的解析式.
(2)结合图象直接写出:当y1>y2时,x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将
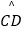 沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC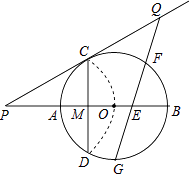
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为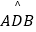 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交
的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交 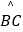 于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?

-
科目: 来源: 题型:
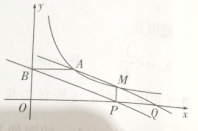
查看答案和解析>>【题目】如图,点A(3,2)和点M(m,n)都在反比例函数y=
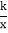 (x>0)的图像上,
(x>0)的图像上,(1)求k的值,并求当m=4时,直线AM的解析式;
(2)过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴于点Q,试说明四边形ABPQ是平行四边形;
(3)在(2)的条件下,四边形ABPQ能否为菱形?若能,请求出m的值;若不是,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求△ABC的周长和面积.

相关试题

