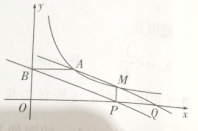
【题目】如图,点A(3,2)和点M(m,n)都在反比例函数y=![]() (x>0)的图像上,
(x>0)的图像上,
(1)求k的值,并求当m=4时,直线AM的解析式;
(2)过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴于点Q,试说明四边形ABPQ是平行四边形;
(3)在(2)的条件下,四边形ABPQ能否为菱形?若能,请求出m的值;若不是,请说明理由.
参考答案:
【答案】(1)k=6,直线AM的解析式为![]() ;(2)详见解析;(3)能,当
;(2)详见解析;(3)能,当![]() 时,四边形ABPQ是菱形.
时,四边形ABPQ是菱形.
【解析】
试题(1)将A坐标代入反比例解析式求出k的值即可;由k的值可得反比例解析式,将m=4代入反比例解析式求出n的值,从而确定M坐标,由待定系数法即可求出直线AM解析式;(2)如图,延长BA、PM相交于N.则∠N=90°,由A(3,2),M(m,n)可得B(0,2),P(m,0),N(m,2).又因点M(m,n)都在反比例函数![]() 的图像上,所以
的图像上,所以![]() ,利用三角函数可得
,利用三角函数可得![]() ,
,![]() ,所以
,所以![]() ,即∠1=∠2,根据同位角相等两直线平行即可得AM∥BP,再由AB∥PQ即可判定四边形ABPQ是平行四边形;(3)当四边形ABPQ是菱形时,PB=AB=3,在直角三角形BOP中,由勾股定理可列方程
,即∠1=∠2,根据同位角相等两直线平行即可得AM∥BP,再由AB∥PQ即可判定四边形ABPQ是平行四边形;(3)当四边形ABPQ是菱形时,PB=AB=3,在直角三角形BOP中,由勾股定理可列方程![]() ,解得m的值即可.
,解得m的值即可.
试题解析:(1)点A(3,2)在反比例函数![]() 的图像上
的图像上
所以![]()
当m=4时,则n=![]() ,所以M(4,
,所以M(4,![]() )
)
设直线AM的解析式为![]()
则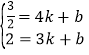
解得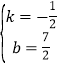
所以直线AM的解析式为![]()
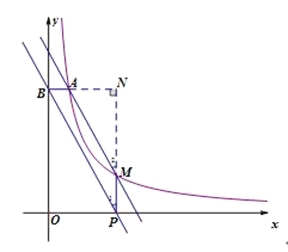
(2)延长BA、PM相交于N.则∠N=90°
∵A(3,2),M(m,n)
∴B(0,2),P(m,0),N(m,2)
∴BN=m,PN=2,AN=m-3,MN=2-n
∴![]()
![]()
∴![]()
∴∠1=∠2
∴AM∥BP
∵AB∥PQ
∴四边形ABPQ是平行四边形
(3)能.当四边形ABPQ是菱形时,PB=AB=3,在直角三角形BOP中,∵![]()
∴![]()
∴![]()
∴当![]() 时,四边形ABPQ是菱形.
时,四边形ABPQ是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将
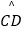 沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC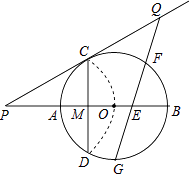
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为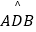 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交
的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交 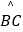 于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,D是BC上的一点,且满足∠BAD=
 ∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
(1)求证:直线BC是⊙O的切线;
(2)连接EF,若tan∠AEF= ,AD=4,求BD的长.
,AD=4,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=30°,∠B=45°,AC=2,求△ABC的周长和面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD边长为1,连接AC,AE平分∠CAD,交BC的延长线于点E,FA⊥AE,交CE于点F,则EF的长为____.
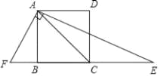
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
求证:(1)△APB≌△DPC;(2)∠BAP=2∠PAC.
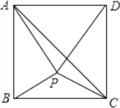
相关试题

