【题目】如图,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=![]() (k为常数,k≠0)的图象交于A、B两点,过点A作AC⊥x轴,垂足为C,连接OA,已知OC=2,tan∠AOC=
(k为常数,k≠0)的图象交于A、B两点,过点A作AC⊥x轴,垂足为C,连接OA,已知OC=2,tan∠AOC=![]() ,B(m,﹣2)
,B(m,﹣2)
(1)求一次函数和反比例函数的解析式.
(2)结合图象直接写出:当y1>y2时,x的取值范围.

参考答案:
【答案】(1)反比例函数的解析式为y=![]() ,一次函数的解析式为y=x+1.(2)x的取值范围为﹣3<x<0或x>2.
,一次函数的解析式为y=x+1.(2)x的取值范围为﹣3<x<0或x>2.
【解析】
(1)求得A(2,3),把A(2,3)代入y2=![]() 可得反比例函数的解析式为y=
可得反比例函数的解析式为y=![]() ,求得B(﹣3,﹣2),把A(2,3),B(﹣3,﹣2)代入一次函数y1=ax+b,可得一次函数的解析式为y=x+1.
,求得B(﹣3,﹣2),把A(2,3),B(﹣3,﹣2)代入一次函数y1=ax+b,可得一次函数的解析式为y=x+1.
(2)由图可得,当y1>y2时,x的取值范围为﹣3<x<0或x>2.
(1)∵OC=2,tan∠AOC=![]() ,
,
∴AC=3,
∴A(2,3),
把A(2,3)代入y2=![]() 可得,k=6,
可得,k=6,
∴反比例函数的解析式为y=![]() ,
,
把B(m,﹣2)代入反比例函数,可得m=﹣3,
∴B(﹣3,﹣2),
把A(2,3),B(﹣3,﹣2)代入一次函数y1=ax+b,可得
![]() ,
,
解得,![]() ,
,
∴一次函数的解析式为y=x+1.
(2)由图可得,当y1>y2时,x的取值范围为﹣3<x<0或x>2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AC,BD是对角线。将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG。则下列结论:①四边形AEGF是菱形;②△AED≌△GED;③∠DFG=112.5°;④BC+FG=1.5.其中正确的结论是( )
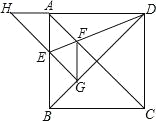
A. ①②③④ B. ①②③ C. ①② D. ②
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O(0,0),A(0,1)是正方形OAA1B的两个顶点,以OA1对角线为边作正方形OA1A2B1,再以正方形的对角线OA2作正方形OA1A2B1,…,依此规律,则点A2017的坐标是( )
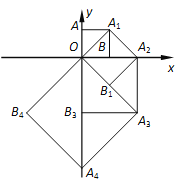
A. (0,21008) B. (21008,21008) C. (21009,0) D. (21009,-21009)
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学知识伴随着人类文明的起源而产生,人类祖先为我们留下了许多珍贵的原始资料,古巴比伦楔形文字泥板书就是其中之一,古巴比伦泥板上记载了两种利用平方数表计算两数乘积的公式:
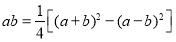 …①
…①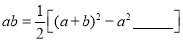 …②
…②(1)材料中,公式②中的空缺部分应该是 ;
(2)请你验证材料中的公式①;
(3)当
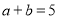 ,
, 时,利用公式①计算
时,利用公式①计算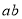 的值为 .
的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将
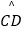 沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC
沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC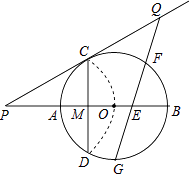
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为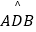 的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交
的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交 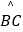 于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由.
于点F(F与B、C不重合).问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AC=BC,D是BC上的一点,且满足∠BAD=
 ∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
(1)求证:直线BC是⊙O的切线;
(2)连接EF,若tan∠AEF= ,AD=4,求BD的长.
,AD=4,求BD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热[此过程中水温y(℃)与开机时间x(分)满足一次函数关系],当加热到100℃时自动停止加热,随后水温开始下降[此过程中水温y(℃)与开机时间x(分)成反比例关系],当水温降至20℃时,饮水机又自动开始加热…,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内的温度约为多少℃?

相关试题

