【题目】正方形ABCD的边长为4,将此正方形置于平面直角坐标系中,使AB边落在X轴的正半轴上,且A点的坐标是(1,0).
(1)直线![]() 经过点C,且与x轴交与点E,求四边形AECD的面积;
经过点C,且与x轴交与点E,求四边形AECD的面积;
(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的解析式;
(3)若直线l1经过点F(﹣![]() ,0),且与直线y=3x平行,将(2)中直线l沿着y轴向上平移
,0),且与直线y=3x平行,将(2)中直线l沿着y轴向上平移![]() 个单位交轴x于点M,交直线l1于点N,求△NMF的面积.
个单位交轴x于点M,交直线l1于点N,求△NMF的面积.

参考答案:
【答案】(1)四边形AECD在面积为10;(2)直线l的解析式为y=2x-4;(3)![]()
【解析】试题分析:(1)由题意知边长已经告诉,易求四边形的面积;
(2)直线l经过点E且将正方形ABCD分成面积相等的两部分,设与DC交于点F,根据正方形的性质,可求出F点坐标,设直线l的解析式是y=kx+b,把E、F的坐标代入即可求出解析式;
(3)根据直线l1经过点F(﹣![]() ,0)且与直线y=3x平行,知k=3,把F的坐标代入即可求出b的值即可得出直线11,同理求出解析式y=2x-3,进一步求出M、N的坐标,利用三角形的面积公式即可求出△MNF的面积.
,0)且与直线y=3x平行,知k=3,把F的坐标代入即可求出b的值即可得出直线11,同理求出解析式y=2x-3,进一步求出M、N的坐标,利用三角形的面积公式即可求出△MNF的面积.
试题解析:(1)在y=![]() x
x![]() 中,令y=4,即
中,令y=4,即![]() x
x![]() =4,解得:x=5,则B的坐标是(5,0);
=4,解得:x=5,则B的坐标是(5,0);
令y=0,即![]() x
x![]() =0,解得:x=2,则E的坐标是(2,0).
=0,解得:x=2,则E的坐标是(2,0).
则OB=5,OE=2,BE=OB﹣OA=5﹣2=3,∴AE=AB﹣BE=4﹣3=1,
四边形AECD的面积=![]() (AE+CD)AD=
(AE+CD)AD=![]() (4+1)×4=10;
(4+1)×4=10;
(2)经过点E且将正方形ABCD分成面积相等的两部分,则直线与CD的交点F,必有CF=AE=1,则F的坐标是(4,4).
设直线的解析式是y=kx+b,则![]() ,解得:
,解得: ![]() .
.
则直线l的解析式是:y=2x﹣4;
(3)∵直线l1经过点F(﹣![]() ,0)且与直线y=3x平行,
,0)且与直线y=3x平行,
设直线11的解析式是y1=kx+b,则:k=3,
代入得:0=3×(﹣![]() )+b,解得:b=
)+b,解得:b=![]() ,
,
∴y1=3x+![]() ,
,
已知将(2)中直线l沿着y轴向上平移![]() 个单位,则所得的直线的解析式是y=2x﹣4+
个单位,则所得的直线的解析式是y=2x﹣4+![]() ,
,
即:y=2x﹣3![]() ,当y=0时,x=
,当y=0时,x=![]() ,∴M(
,∴M(![]() ,0),
,0),
解方程组 得:
得: 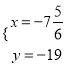 ,即:N(﹣7
,即:N(﹣7![]() ,﹣19),
,﹣19),
S△NMF=![]() ×[
×[![]() ﹣(﹣
﹣(﹣![]() )]×|﹣19|=
)]×|﹣19|=![]() .
.
答:△NMF的面积是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点A的坐标为(1,0),点B的坐标为(3,2),将点A向左平移两个单位,再向上平移4个单位得到点C.
(1)写出点C的坐标,并作出三角形ABC;
(2)求三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果将抛物线y=x2+2向左平移1个单位,那么所得新抛物线的解析式为( )
A.y=(x﹣1)2+2B.y=(x+1)2+2C.y=x2+1D.y=x2+3
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣(﹣1)﹣
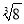 +(π﹣3.14)0;
+(π﹣3.14)0;(2)2×(1﹣
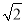 )+
)+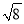 ;
;(3)
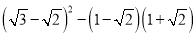 ;
;(4)
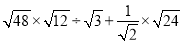 ;
;(5)
 ;
;(6)
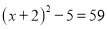 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(原创题)如图所示,在书写艺术字时,常常运用画“平行线段”这种基本作图方法,此图是在书写字“M”:

(1)请从正面,上面,右侧三个不同方向上各找出一组平行线段,并用字母表示出来;
(2)EF与A′B′有何位置关系?CC′与DH有何位置关系? -
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.2a+2a=2a2
B.(a3)3=a9
C.a2a4=a8
D.a6÷a3=a2 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读探索题:(1)如图
 ,
,  是
是 的平分线,以
的平分线,以 为圆心任意长为半径作弧,分别交射线
为圆心任意长为半径作弧,分别交射线 、
、 于
于 、
、 两点,在射线
两点,在射线 上任取一点
上任取一点 (点
(点 除外),连接
除外),连接 、
、 .求证:
.求证:  ≌
≌ .
.(2)请你参考以上方法,解答下列问题:
如图2,在
 中,
中,  ,
,  ,
,  平分
平分 ,试判断
,试判断 和
和 、
、 之间的数量关系并证明.
之间的数量关系并证明.


相关试题

