【题目】在平面直角坐标系xOy中,点A的坐标为(1,0),点B的坐标为(3,2),将点A向左平移两个单位,再向上平移4个单位得到点C.
(1)写出点C的坐标,并作出三角形ABC;
(2)求三角形ABC的面积.
参考答案:
【答案】(1)C(﹣1,4);(2)6.
【解析】试题分析:(1)根据点的平移规律,上加下减,左减右加即可得;
(2)先补形,然后用正方形的面积减去多余的三角形面积即可得.
试题解析:(1)点A的坐标为(1,0),将点A向左平移两个单位,再向上平移4个单位得到点C,所以点C的坐标为:(1-2,0+4),即C(﹣1,4);
(2)如图,过点B作BD⊥x轴于D,过点C分别作x轴,y轴的垂线,与x轴交于点E,与BD交于点F.
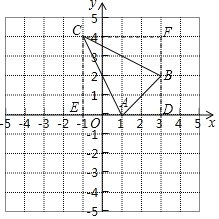
∵点B,C的坐标分别为(3,2),(﹣1,4),
∴点D,E,F的坐标分别为(3,0),(﹣1,0),(3,4),
∴AD=AE=BD=BF=2,CE=CF=DE=DF=4,
∴正方形CFDE的面积为16,
∵△ACE的面积为4,△ABD的面积为2,△BCF的面积为4.
∴△ABC的面积为16﹣4﹣2﹣4=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列三个日常现象:
①用两根钉子就可以把一根木条固定在墙上
②把弯曲的公路改直,就能够缩短路程
③从A地到B地架设电线,总是尽可能沿着线段AB来架设
其中,可以用“两点之间,线段最短”来解释的现象是______(填序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a﹣1=(﹣1)0,则a=__.
-
科目: 来源: 题型:
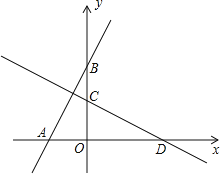
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,过点A(﹣2,0)的直线交y轴正半轴于点B(0,4),将直线AB绕着点O顺时针旋转90°后,分别与x轴、y轴交于点D、C.且点C(0,3).
(1)求直线AB的函数关系式;
(2)连接BD,求△ABD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果将抛物线y=x2+2向左平移1个单位,那么所得新抛物线的解析式为( )
A.y=(x﹣1)2+2B.y=(x+1)2+2C.y=x2+1D.y=x2+3
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣(﹣1)﹣
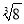 +(π﹣3.14)0;
+(π﹣3.14)0;(2)2×(1﹣
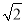 )+
)+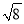 ;
;(3)
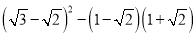 ;
;(4)
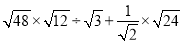 ;
;(5)
 ;
;(6)
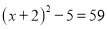 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】正方形ABCD的边长为4,将此正方形置于平面直角坐标系中,使AB边落在X轴的正半轴上,且A点的坐标是(1,0).
(1)直线
 经过点C,且与x轴交与点E,求四边形AECD的面积;
经过点C,且与x轴交与点E,求四边形AECD的面积;(2)若直线l经过点E,且将正方形ABCD分成面积相等的两部分,求直线l的解析式;
(3)若直线l1经过点F(﹣
 ,0),且与直线y=3x平行,将(2)中直线l沿着y轴向上平移
,0),且与直线y=3x平行,将(2)中直线l沿着y轴向上平移 个单位交轴x于点M,交直线l1于点N,求△NMF的面积.
个单位交轴x于点M,交直线l1于点N,求△NMF的面积.
相关试题

