【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,下面四个结论正确的有________________.
①BP=CM;②△ABQ≌△CAP;③∠CMQ的度数不变,始终等于60°;④当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形.
秒时,△PBQ为直角三角形.

参考答案:
【答案】②③④
【解析】∵点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,
∴AP=BQ,∠ABQ=∠CAP=60°,AB=CA,BP=CQ,
∴△ABQ≌△CAP.(即结论②成立);
∴∠BAQ=∠ACP,
∵∠CMQ=∠ACP+∠CAM,
∴∠CMQ=∠BAQ+∠CAM=∠CAP=60°.(即结论③成立);
又∵∠MQC>∠ABQ=60°,
∴∠MQC>∠CMQ,
∴MC>QC,即MC>BP.(即结论①不成立);
设t秒时,△BPQ是直角三角形,此时AP=BQ=t,BP=4-t,
(1)当∠PQB=90°,∵∠PBQ=60°,
∴∠BPQ=30°,
∴BQ=![]() PB,即
PB,即![]() ,解得:
,解得: ![]() ;
;
(2)当∠QPB=90°时,∵∠PBQ=60°,
∴∠PQB=30°,
∴BP=![]() BQ,即
BQ,即![]() ,解得:
,解得: ![]() .
.
结合(1)、(2)可得:当![]() 或
或![]() 时,△BPQ是直角三角形.(即结论④成立);
时,△BPQ是直角三角形.(即结论④成立);
综上所述,正确的结论是:②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某游泳池长48米,小方和小杨进行游泳比赛,从同一处(A点)出发,小方平均速度为3米/秒,小杨为3.1米/秒.但小杨一心想快,不看方向沿斜线(AC方向)游,而小方直游(AB方向),两人到达终点的位置相距14米.按各人的平均速度计算,谁先到达终点,为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆分别交AC,BC边于点D,E,连接BD,
(1)求证:点E是
 的中点;
的中点;(2)当BC=12,且AD:CD=1:2时,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,BA=BC,∠ABC=40°,∠ABC的平分线与BC的垂直平分线交于点O,E在BC边上,F在AC边上,将∠A沿直线EF翻折,使点A与点O恰好重合,则∠OEF的度数是_____.

-
科目: 来源: 题型:
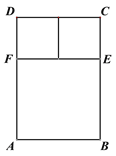
查看答案和解析>>【题目】如图是一种窗框的设计示意图,矩形ABCD被分成上下两部分,上部的矩形CDFE由两个正方形组成,制作窗框的材料总长为6m.
(1)若AB为1m,直接写出此时窗户的透光面积__________m2;
(2)设AB=x,求窗户透光面积S关于x的函数表达式,并求出S的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,O是AC与BD的交点,过O点的直线EF与AB,CD的延长线分别交于E,F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么关系时,以A,E,C,F为顶点的四边形是菱形?证明你的结论.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 轴相交于点A、B,且过点C(4,3).
轴相交于点A、B,且过点C(4,3).(1)求
 的值和该抛物线顶点P的坐标;
的值和该抛物线顶点P的坐标;(2)将该抛物线向左平移,记平移后抛物线的顶点为P′,当四边形AP′PB为平行四边形时,求平移后抛物线的解析式.

相关试题

