搜索
【题目】如图，某游泳池长48米，小方和小杨进行游泳比赛，从同一处（A点）出发，小方平均速度为3米/秒，小杨为3.1米/秒．但小杨一心想快，不看方向沿斜线（AC方向）游，而小方直游（AB方向），两人到达终点的位置相距14米．按各人的平均速度计算，谁先到达终点，为什么？
参考答案：
【答案】小方先到达终点．
【解析】试题分析：根据题中已知条件，利用勾股定理将AC边的长求出来，然后将两人所游的距离除以各自的游泳速度，计算出到达中点所需的时间，进行比较即可．
试题解析：
如图，AB表示小方的路线，AC表示小杨的路线，
由题意可知，AB=48，BC=14，
在直角三角形ABC中，AC=
=50，
小方用时：
=16秒，小杨用时
秒，
因为16
，所以小方用时少，即小方先到达终点．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将n张长度为a的长方形纸条，一张接一张地粘成长纸条，粘合部分的长度都是2，则这张纸条的总长度是____________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线AB与x轴交于点A（1，0），与y轴交于点B（0，﹣2）．
（1）求直线AB的解析式；
（2）若直线AB上的点C在第一象限，且S△BOC=2，求点C的坐标．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A是抛物线
对称轴上的一点，连接OA，以A为旋转中心将AO逆时针旋转90°得到AO′，当O′恰好落在抛物线上时，点A的坐标为______________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=AC，以AB为直径的半圆分别交AC，BC边于点D，E，连接BD，
（1）求证：点E是
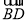的中点；（2）当BC=12，且AD:CD=1:2时，求⊙O的半径．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，BA=BC，∠ABC=40°，∠ABC的平分线与BC的垂直平分线交于点O，E在BC边上，F在AC边上，将∠A沿直线EF翻折，使点A与点O恰好重合，则∠OEF的度数是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，下面四个结论正确的有________________．
①BP=CM；②△ABQ≌△CAP；③∠CMQ的度数不变，始终等于60°；④当第
秒或第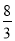
秒时，△PBQ为直角三角形．
相关试题
