【题目】阅读下面材料:
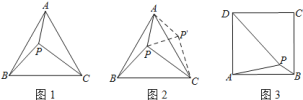
小伟遇到这样一个问题:如图![]() ,在正三角形
,在正三角形![]() 内有一点
内有一点![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.小伟是这样思考的:如图
的度数.小伟是这样思考的:如图![]() ,利用旋转和全等的知识构造
,利用旋转和全等的知识构造![]() ,连接
,连接![]() ,得到两个特殊的三角形,从而将问题解决.
,得到两个特殊的三角形,从而将问题解决.
(1)请你回答:图![]() 中
中![]() 的度数等于________.
的度数等于________.
参考小伟同学思考问题的方法,解决下列问题:
(2)如图![]() ,在正方形
,在正方形![]() 内有一点
内有一点![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数和正方形的边长.
的度数和正方形的边长.
参考答案:
【答案】150°
【解析】
把△APB绕点A逆时针旋转60°得到△![]() ,根据旋转的性质可得P
,根据旋转的性质可得P![]() A=PA,P
A=PA,P![]() C=PB,∠PAP
C=PB,∠PAP![]() =60°,再用勾股定理得出∠P
=60°,再用勾股定理得出∠P![]() PC=90°,然后求出∠AP
PC=90°,然后求出∠AP![]() C,即为∠APB的度数;把
C,即为∠APB的度数;把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,由旋转的性质,
,由旋转的性质,![]() ,
,![]() ,
,![]() ,然后判断出△APP
,然后判断出△APP![]() 是等腰三角形,根据等腰三角形性质求出PP
是等腰三角形,根据等腰三角形性质求出PP![]() ,∠PAP
,∠PAP![]() =45°,再运用勾股定理逆定理得出∠PP
=45°,再运用勾股定理逆定理得出∠PP![]() D=90°,然后求∠AP
D=90°,然后求∠AP![]() D,即为∠APB度数,在求出P
D,即为∠APB度数,在求出P![]() ,P,B三点共线,过点A作AE⊥PP
,P,B三点共线,过点A作AE⊥PP![]() 于E,根据等腰三角的性质求出AE,然后求BE,在直角三角形ABE中,利用勾股定理求出AB即可.
于E,根据等腰三角的性质求出AE,然后求BE,在直角三角形ABE中,利用勾股定理求出AB即可.
(1)![]() .
.
![]() 如图
如图![]() ,把
,把![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,
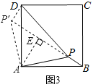
由旋转的性质,![]() ,
,![]() ,
,![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]() ,
,
∵![]() ,
,
∴点![]() 、
、![]() 、
、![]() 三点共线,
三点共线,
过点![]() 作
作![]() 于
于![]() ,
,
则![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知在平面直角坐标系中,A(
 ,0),B(4,0),C(0,3),过点C作CD∥x轴,与直线AD交于点D,直线AD与y轴交于点E,连接AC、BD,且tan∠DAB=
,0),B(4,0),C(0,3),过点C作CD∥x轴,与直线AD交于点D,直线AD与y轴交于点E,连接AC、BD,且tan∠DAB= .
.
(1)求直线AD的解析式和线段BD所在直线的解析式.
(2)如图2,将△CAD沿着直线CD向右平移得△C1A1D1,当C1A1⊥EA1时,在x轴上是否存在点M,使△A1D1M是以A1D1为腰的等腰三角形,若存在,求出△A1D1M的周长;若不存在,请说明理由.
(3)如图3,延长DB至F,使得BF=DB,点K为线段AD上一动点,连接KF、BK,将△FBK沿BK翻折得△F′BK,请直接写出当DK为何值时,△F′BK与△DBK的重叠部分的面积恰好是△FKD的面积的
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
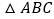 中,
中,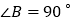 ,
,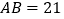 ,
,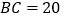 .若有一半径为
.若有一半径为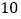 的圆分别与
的圆分别与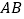 、
、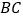 相切,则下列何种方法可找到此圆的圆心( )
相切,则下列何种方法可找到此圆的圆心( )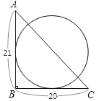
A.
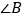 的角平分线与
的角平分线与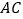 的交点 B.
的交点 B. 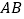 的中垂线与
的中垂线与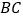 中垂线的交点
中垂线的交点C.
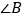 的角平分线与
的角平分线与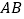 中垂线的交点 D.
中垂线的交点 D. 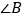 的角平分线与
的角平分线与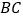 中垂线的交点
中垂线的交点 -
科目: 来源: 题型:
查看答案和解析>>【题目】(2011?常州)如图,DE是⊙O的直径,弦AB⊥CD,垂足为C,若AB=6,CE=1,则OC= ,CD= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①、②、③,正三角形
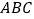 、正方形
、正方形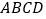 、正五边形
、正五边形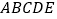 分别是
分别是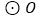 的内接三角形、内接四边形、内接五边形,点
的内接三角形、内接四边形、内接五边形,点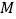 、
、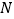 分别从点
分别从点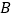 、
、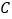 开始,以相同的速度中
开始,以相同的速度中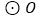 上逆时针运动.如图①、②、③,正三角形
上逆时针运动.如图①、②、③,正三角形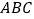 、正方形
、正方形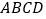 、正五边形
、正五边形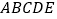 分别是
分别是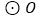 的内接三角形、内接四边形、内接五边形,点
的内接三角形、内接四边形、内接五边形,点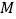 、
、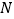 分别从点
分别从点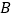 、
、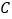 开始,以相同的速度中
开始,以相同的速度中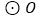 上逆时针运动.
上逆时针运动.(1)求图①中
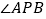 的度数;
的度数;(2)图②中,
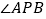 的度数是________,图③中
的度数是________,图③中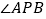 的度数是________;
的度数是________;(3)根据前面探索,你能否将本题推广到一般的正
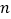 边形情况?若能,写出推广问题和结论;若不能,请说明理由.
边形情况?若能,写出推广问题和结论;若不能,请说明理由.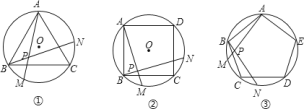
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形
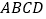 是平行四边形,要使它成为菱形,那么需要添加的条件可以是( )
是平行四边形,要使它成为菱形,那么需要添加的条件可以是( )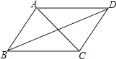
A.
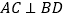 B.
B. 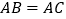 C.
C. 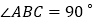 D.
D. 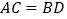
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小华剪了两条宽为1的纸条,交叉叠放在一起,且它们较小的交角为60°,则它们重叠部分的面积为( )

A. 3 B. 2 C.
 D.
D. 
相关试题

