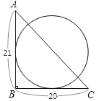
【题目】如图所示,![]() 中,
中,![]() ,
,![]() ,
,![]() .若有一半径为
.若有一半径为![]() 的圆分别与
的圆分别与![]() 、
、![]() 相切,则下列何种方法可找到此圆的圆心( )
相切,则下列何种方法可找到此圆的圆心( )
A. ![]() 的角平分线与
的角平分线与![]() 的交点 B.
的交点 B. ![]() 的中垂线与
的中垂线与![]() 中垂线的交点
中垂线的交点
C. ![]() 的角平分线与
的角平分线与![]() 中垂线的交点 D.
中垂线的交点 D. ![]() 的角平分线与
的角平分线与![]() 中垂线的交点
中垂线的交点
参考答案:
【答案】D
【解析】
因为圆分别与AB、BC相切,所以圆心到AB、CB的距离一定相等,都等于半径.而到角的两边距离相等的点在角的平分线上,圆的半径为10,所以圆心到AB的距离为10.因为![]() ,所以BC的中垂线上的点到AB的距离为10,所以
,所以BC的中垂线上的点到AB的距离为10,所以![]() 的角平分线与BC的中垂线的交点即为圆心.
的角平分线与BC的中垂线的交点即为圆心.
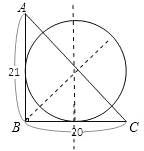
![]() 圆分别与AB、BC相切,
圆分别与AB、BC相切,![]() 圆心到AB、CB的距离都等于半径,
圆心到AB、CB的距离都等于半径,![]() 到角的两边距离相等的点在角的平分线上,
到角的两边距离相等的点在角的平分线上,![]() 圆心定在
圆心定在![]() 的角平分线上,
的角平分线上,![]() 因为圆的半径为10,
因为圆的半径为10,![]() 圆心到AB的距离为10,
圆心到AB的距离为10,![]() ,
,
又![]() ,
,![]() 的中垂线上的点到AB的距离为10,
的中垂线上的点到AB的距离为10,![]() 的角平分线与BC的中垂线的交点即为圆心.
的角平分线与BC的中垂线的交点即为圆心.
所以D选项是正确的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】创意产品蕴含着很多商机,我市某文化创意公司,销售A,B两种创意产品,其中A产品的定价是每件20元,B产品的定价是每件30元.
(1)该公司按定价售出A,B两种产品共600件,若销售总额不低于15000元,则至少销售B产品多少件?
(2)2017年8月,该公司按定价售出A产品300件,B产品400件.2017年9月,公司根据市场情况,适当调整A,B产品的售价,A产品的售价比定价增加了a%,销量与8月保持不变;B产品的售价比定价减少了a%,销量比8月份增加了a%,结果9月份A,B产品的销售总额比8月份增加了
 a%,求a的值.
a%,求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一个三位正整数n各数位上的数字重新排列(含n本身)后,得到新的三位数
 (a<c),在所有重新排列大的数中,当|a+c﹣2b|最小时,我们称
(a<c),在所有重新排列大的数中,当|a+c﹣2b|最小时,我们称 是n的“天时数”,并规定F(n)=b2﹣ac.当|a+c﹣2b|最大时,我们称
是n的“天时数”,并规定F(n)=b2﹣ac.当|a+c﹣2b|最大时,我们称 是n的“地利数”,并规定G(n)=ac﹣b2.并规定M(n)=
是n的“地利数”,并规定G(n)=ac﹣b2.并规定M(n)= 是n的“人和数”,例如:215可以重新排列为125,152,215,因为|1+5﹣2×2|=2,|1+2﹣2×5|=7,|2+5﹣2×1|=5,且2<5<7,所以125是215的“天时数”F(125)=22﹣1×5=﹣1,152是215的“地利数”,G(152)=1×2﹣52=﹣23,M(215)=
是n的“人和数”,例如:215可以重新排列为125,152,215,因为|1+5﹣2×2|=2,|1+2﹣2×5|=7,|2+5﹣2×1|=5,且2<5<7,所以125是215的“天时数”F(125)=22﹣1×5=﹣1,152是215的“地利数”,G(152)=1×2﹣52=﹣23,M(215)=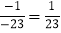 .
.(1)计算:F(168),G(168);
(2)设三位自然数s=100x+50+y(1≤x≤9,1≤y≤9,且x,y均为正整数),交换其个位上的数字与百位上的数字得到t,若s﹣t=693,那么我们称s为“厚积薄发数”;请求出所有“厚积薄发数”中M(s)的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知在平面直角坐标系中,A(
 ,0),B(4,0),C(0,3),过点C作CD∥x轴,与直线AD交于点D,直线AD与y轴交于点E,连接AC、BD,且tan∠DAB=
,0),B(4,0),C(0,3),过点C作CD∥x轴,与直线AD交于点D,直线AD与y轴交于点E,连接AC、BD,且tan∠DAB= .
.
(1)求直线AD的解析式和线段BD所在直线的解析式.
(2)如图2,将△CAD沿着直线CD向右平移得△C1A1D1,当C1A1⊥EA1时,在x轴上是否存在点M,使△A1D1M是以A1D1为腰的等腰三角形,若存在,求出△A1D1M的周长;若不存在,请说明理由.
(3)如图3,延长DB至F,使得BF=DB,点K为线段AD上一动点,连接KF、BK,将△FBK沿BK翻折得△F′BK,请直接写出当DK为何值时,△F′BK与△DBK的重叠部分的面积恰好是△FKD的面积的
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2011?常州)如图,DE是⊙O的直径,弦AB⊥CD,垂足为C,若AB=6,CE=1,则OC= ,CD= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
小伟遇到这样一个问题:如图
 ,在正三角形
,在正三角形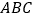 内有一点
内有一点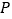 ,且
,且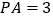 ,
,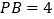 ,
,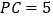 ,求
,求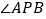 的度数.小伟是这样思考的:如图
的度数.小伟是这样思考的:如图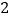 ,利用旋转和全等的知识构造
,利用旋转和全等的知识构造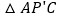 ,连接
,连接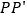 ,得到两个特殊的三角形,从而将问题解决.
,得到两个特殊的三角形,从而将问题解决.(1)请你回答:图
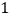 中
中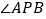 的度数等于________.
的度数等于________.参考小伟同学思考问题的方法,解决下列问题:
(2)如图
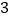 ,在正方形
,在正方形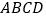 内有一点
内有一点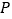 ,且
,且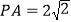 ,
,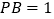 ,
,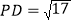 ,求
,求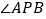 的度数和正方形的边长.
的度数和正方形的边长.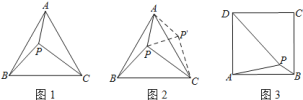
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①、②、③,正三角形
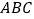 、正方形
、正方形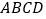 、正五边形
、正五边形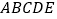 分别是
分别是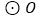 的内接三角形、内接四边形、内接五边形,点
的内接三角形、内接四边形、内接五边形,点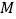 、
、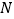 分别从点
分别从点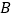 、
、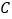 开始,以相同的速度中
开始,以相同的速度中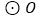 上逆时针运动.如图①、②、③,正三角形
上逆时针运动.如图①、②、③,正三角形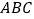 、正方形
、正方形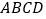 、正五边形
、正五边形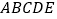 分别是
分别是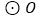 的内接三角形、内接四边形、内接五边形,点
的内接三角形、内接四边形、内接五边形,点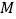 、
、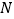 分别从点
分别从点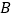 、
、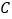 开始,以相同的速度中
开始,以相同的速度中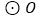 上逆时针运动.
上逆时针运动.(1)求图①中
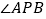 的度数;
的度数;(2)图②中,
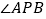 的度数是________,图③中
的度数是________,图③中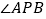 的度数是________;
的度数是________;(3)根据前面探索,你能否将本题推广到一般的正
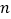 边形情况?若能,写出推广问题和结论;若不能,请说明理由.
边形情况?若能,写出推广问题和结论;若不能,请说明理由.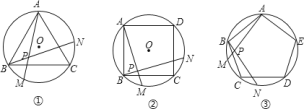
相关试题

