【题目】如图,已知AB ![]() ,在AB,CD之间取一点E,连接EA,EC,试探索
,在AB,CD之间取一点E,连接EA,EC,试探索![]() AEC与
AEC与![]() EAB,
EAB,![]() ECD之间的关系
ECD之间的关系![]() 若点E取在AC上
若点E取在AC上![]() 如图
如图![]() ,则
,则![]() AEC
AEC![]() ,由此可得
,由此可得![]() AEC
AEC![]() EAB
EAB![]() ECD或
ECD或![]() AEC
AEC![]() EAB
EAB![]() ECD
ECD![]() 如果点E取在AC的两侧
如果点E取在AC的两侧![]() 如图
如图![]() ,结论会是什么?
,结论会是什么?

参考答案:
【答案】图②,![]() AEC
AEC![]() EAB
EAB![]() ECD;图③,
ECD;图③,![]() AEC
AEC![]() EAB
EAB![]() ECD
ECD![]()
【解析】试题分析:如图②,过点E作EF∥AB,交AC于点F,由AB∥CD,可得AB∥EF∥CD,根据两直线平行,内错角相等,可得∠AEC=∠EAB+∠ECD;如图③,过点E作EF∥AB,交AC于点F,由AB∥CD,可得AB∥EF∥CD,根据两直线平行,同旁内角互补,即可证得∠EAB+∠ECD+∠AEC=360°.
试题解析:
如图②,过点E作EF∥AB,交AC于点F,

∵AB∥CD,
∴AB∥EF∥CD,
∴∠EAB=∠AEF,∠ECD=∠FEC,
∴∠AEC=∠EAB+∠ECD;
如图③,过点E作EF∥AB,交AC于点F,
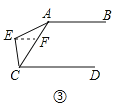
∵AB∥CD,
∴AB∥EF∥CD,
∴∠EAB+∠AEF=180°,∠ECD+∠CEF=180°,
∴∠EAB+∠ECD+∠AEC=360°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=2 a -7,B=a2- 4a+3,C= a2 +6a-28,其中
 .
.(1)求证:B-A>0,并指出A与B的大小关系;
(2)阅读对B因式分解的方法:
解:B=a2- 4a+3=a2- 4a+4-1=(a-2)2-1=(a-2+1)(a-2-1)=(a-1)(a-3).
请完成下面的两个问题:
①仿照上述方法分解因式:x2- 4x-96;
②指出A与C哪个大?并说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知直线l1
 l2,且l3和l1,l2分别交于A、B两点,点P在直线AB上
l2,且l3和l1,l2分别交于A、B两点,点P在直线AB上

 试找出
试找出 之间的关系并说明理由;
之间的关系并说明理由; 当点P在A,B两点间运动时,问
当点P在A,B两点间运动时,问 之间的关系是否发生变化?
之间的关系是否发生变化? 如果点P在A,B两点外侧运动时,试探究
如果点P在A,B两点外侧运动时,试探究 之间的关系
之间的关系 只写结论,不需要说明理由,并在备用图①、②中画出对应图形
只写结论,不需要说明理由,并在备用图①、②中画出对应图形 .
.
-
科目: 来源: 题型:
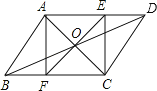
查看答案和解析>>【题目】在平行四边形ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC,
求证:四边形AFCE是矩形.
-
科目: 来源: 题型:
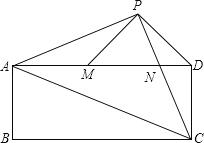
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
(1)若AP=
 ,AB=
,AB= BC,求矩形ABCD的面积;
BC,求矩形ABCD的面积;(2)若CD=PM,求证:AC=AP+PN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P(3a﹣2,2a+7)在第二、四象限的角平分线上,则点P的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市准备购进A、B两种品牌台灯,其中A每盏进价比B进价贵30元,A售价120元,B售价80元.已知用1040元购进的A数量与用650元购进B的数量相同.
(1)求A、B的进价;
(2)超市打算购进A、B台灯共100盏,要求A、B的总利润不得少于3400元,不得多于3550元,问有多少种进货方案?
(3)在(2)的条件下,该超市决定对A进行降价促销,A台灯每盏降价m(8<m<15)元,B不变,超市如何进货获利最大?
相关试题

