【题目】如图,己知直线l1![]() l2,且l3和l1,l2分别交于A、B两点,点P在直线AB上
l2,且l3和l1,l2分别交于A、B两点,点P在直线AB上![]()

![]() 试找出
试找出![]() 之间的关系并说明理由;
之间的关系并说明理由;
![]() 当点P在A,B两点间运动时,问
当点P在A,B两点间运动时,问![]() 之间的关系是否发生变化?
之间的关系是否发生变化?
![]() 如果点P在A,B两点外侧运动时,试探究
如果点P在A,B两点外侧运动时,试探究![]() 之间的关系
之间的关系![]() 只写结论,不需要说明理由,并在备用图①、②中画出对应图形
只写结论,不需要说明理由,并在备用图①、②中画出对应图形![]() .
.

参考答案:
【答案】(1)∠1+∠2=∠3;![]() 不发生变化;(3)∠1-∠2=∠3或∠2-∠1=∠3;;
不发生变化;(3)∠1-∠2=∠3或∠2-∠1=∠3;;
【解析】试题分析:(1)过点P作l1的平行线,根据平行线的性质即可解决问题.(2)(3)类比(1)的方法解决即可.
试题解析:
(1)∠1+∠2=∠3;
理由:如图,过点P作l1的平行线,
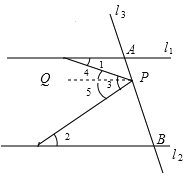
∵l1∥l2,
∴l1∥l2∥PQ,
∴∠1=∠4,∠2=∠5,(两直线平行,内错角相等)
∵∠4+∠5=∠3,
∴∠1+∠2=∠3;
(2)同(1)可证:∠1+∠2=∠3;
(3)∠1-∠2=∠3或∠2-∠1=∠3
理由:当点P在下侧时,过点P作l1的平行线PQ,
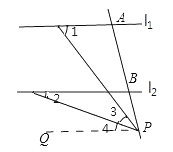
∵l1∥l2,
∴l1∥l2∥PQ,
∴∠2=∠4,∠1=∠3+∠4,(两直线平行,内错角相等)
∴∠1-∠2=∠3;
当点P在上侧时,同理可得:∠2-∠1=∠3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,下列各点位于x轴上的是( )
A.(1,﹣2)B.(3,0)C.(﹣1,3)D.(0,﹣4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个口袋中有红球、白球共10个,这些球除颜色外都相同.将口袋中的球搅拌均匀,从中随机摸出一个球,记下它的颜色后再放回口袋中,不断重复这一过程,共摸了100次球,发现有70次摸到红球.请你估计这个口袋中有_____个白球.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=2 a -7,B=a2- 4a+3,C= a2 +6a-28,其中
 .
.(1)求证:B-A>0,并指出A与B的大小关系;
(2)阅读对B因式分解的方法:
解:B=a2- 4a+3=a2- 4a+4-1=(a-2)2-1=(a-2+1)(a-2-1)=(a-1)(a-3).
请完成下面的两个问题:
①仿照上述方法分解因式:x2- 4x-96;
②指出A与C哪个大?并说明你的理由.
-
科目: 来源: 题型:
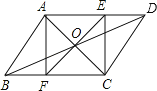
查看答案和解析>>【题目】在平行四边形ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC,
求证:四边形AFCE是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB
 ,在AB,CD之间取一点E,连接EA,EC,试探索
,在AB,CD之间取一点E,连接EA,EC,试探索 AEC与
AEC与 EAB,
EAB, ECD之间的关系
ECD之间的关系 若点E取在AC上
若点E取在AC上 如图
如图 ,则
,则 AEC
AEC ,由此可得
,由此可得 AEC
AEC EAB
EAB ECD或
ECD或 AEC
AEC EAB
EAB ECD
ECD 如果点E取在AC的两侧
如果点E取在AC的两侧 如图
如图 ,结论会是什么?
,结论会是什么?
-
科目: 来源: 题型:
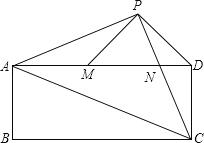
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,AC是对角线.点P为矩形外一点且满足AP=PC,AP⊥PC.PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
(1)若AP=
 ,AB=
,AB= BC,求矩形ABCD的面积;
BC,求矩形ABCD的面积;(2)若CD=PM,求证:AC=AP+PN.
相关试题

