搜索
【题目】若点P（3a﹣2，2a+7）在第二、四象限的角平分线上，则点P的坐标是_____．
参考答案：
【答案】（﹣5，5）．
【解析】
根据第二、四象限的角平分线上的点，横纵坐标互为相反数，由此可列出关于a的方程，解出a的值即可求得点P的坐标．
∵点P（3a﹣2，2a+7）在第二、四象限的角平分线上，
∴3a﹣2+2a+7＝0，
解得：a＝﹣1，
∴P（﹣5，5）．
故答案为：（﹣5，5）．
-
科目： 来源： 题型：
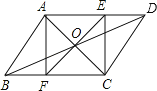
查看答案和解析>>【题目】在平行四边形ABCD中，对角线AC、BD相交于O，EF过点O，且AF⊥BC，
求证：四边形AFCE是矩形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AB
，在AB，CD之间取一点E，连接EA，EC，试探索
AEC与 EAB， ECD之间的关系
若点E取在AC上
如图
，则 AEC
，由此可得 AEC
EAB
ECD或 AEC EAB ECD
如果点E取在AC的两侧如图
，结论会是什么？
-
科目： 来源： 题型：
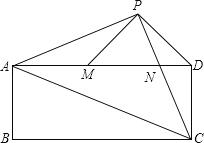
查看答案和解析>>【题目】已知：如图，在矩形ABCD中，AC是对角线．点P为矩形外一点且满足AP=PC，AP⊥PC．PC交AD于点N，连接DP，过点P作PM⊥PD交AD于M．
（1）若AP=
，AB=
BC，求矩形ABCD的面积；（2）若CD=PM，求证：AC=AP+PN．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某超市准备购进A、B两种品牌台灯，其中A每盏进价比B进价贵30元，A售价120元，B售价80元.已知用1040元购进的A数量与用650元购进B的数量相同.
（1）求A、B的进价；
（2）超市打算购进A、B台灯共100盏，要求A、B的总利润不得少于3400元，不得多于3550元，问有多少种进货方案？
（3）在（2）的条件下，该超市决定对A进行降价促销，A台灯每盏降价m（8＜m＜15）元，B不变，超市如何进货获利最大？
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算：（1）（﹣2）2﹣（3﹣5）﹣
+2×（﹣3）；（2）|1﹣
|+|﹣
|+|﹣2|；（3）4（x+3）2﹣16=0；
（4）27（x﹣3）3=﹣8．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知直线y=2x+2与y轴、x轴分别交于A、B两点，以B为直角顶点在第二象限作等腰Rt△ABC ．
（1）求点C的坐标，并求出直线AC的关系式．
（2）如图2，直线CB交y轴于E，在直线CB上取一点D，连接AD，若AD=AC，求证：BE=DE．
（3）如图3，在（1）的条件下，直线AC交x轴于M，P（
，k）是线段BC上一点，在线段BM上是否存在一点N，使△BPN的面积等于△BCM面积的
？若存在，请求出点N的坐标；若不存在，请说明理由．
相关试题
