【题目】如图所示,在Rt△ABC中,∠C=90°,BC=6,AC=8, P是斜边AB上一动点,PD⊥AC于点D,PE⊥BC于点E,则DE的长不可能是( )
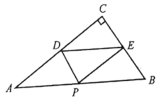
A.4B.5C.6D.7
参考答案:
【答案】A
【解析】
连接CP,根据矩形的性质可知:DE=CP,当DE最小时,则CP最小,根据垂线段最短可知当CP⊥AB时,则CP最小,再根据三角形的面积为定值即可求出CP的长,从而求出DE的最小值,再进行判断即可.
∵Rt△ABC中,∠C=90°,AC=8,BC=6,
∴AB=10,
连接CP,
∵PD⊥AC于点D,PE⊥CB于点E,
∴四边形DPEC是矩形,
∴DE=CP,
当CP最小时,则DE最小,根据垂线段最短可知当CP⊥AB时,则CP最小,
∴![]() ,
,
在四个选项中,只有选项A的值小于4.8,因此,选项A符合题意,
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知正方形ABCD的顶点A,B分别在y轴和x轴上,边CD交x轴的正半轴于点E.
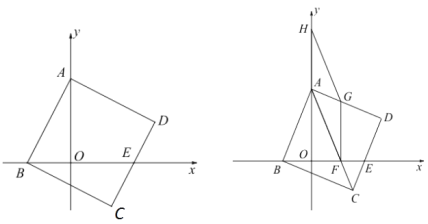
(1)若A(0,a),且
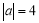 ,求A点的坐标;
,求A点的坐标;(2)在(l)的条件下,若3AO=4EO,求D点的坐标;
(3)如图2,连结AC交x轴于点F,点H是A点上方y轴上一动点,以AF、AH为边作平行四边形AFGH,使G点恰好落在AD边上,试探讨BF,HG与DG的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L上有三个正方形a,b,c,若a,c的面积分别为1和9,则b的面积为( )

A.8 B.9 C.10 D.11
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=4,射线BQ和AB互相垂直,点D是AB上的一个动点,点E在射线BQ上,BE=
 DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BQ于点C.设BE=x,BC=y,则y关于x的函数解析式为______________.
DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BQ于点C.设BE=x,BC=y,则y关于x的函数解析式为______________.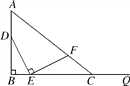
-
科目: 来源: 题型:
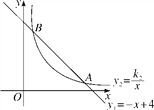
查看答案和解析>>【题目】如图,函数y1=-x+4的图象与函数y2=
 (x>0)的图象交于A(a,1)、B(1,b)两点.
(x>0)的图象交于A(a,1)、B(1,b)两点.(1)求函数y2的表达式;
(2)观察图象,比较当x>0时,y1与y2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):
第1批
第2批
第3批
第4批
第5批
3 km
10 km
-4 km
-3 km
-7 km
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)该驾驶员离公司距离最远是多少千米?
(3)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,O在AB上,以O为圆心,OB长为半径的圆与BC交于点D,DE⊥AC于E.
(1)求证:DE是⊙O的切线;
(2)若AC与⊙O相切于F,AB=5,sinA=
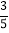 ,求⊙O的半径.
,求⊙O的半径.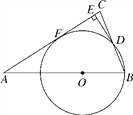
相关试题

