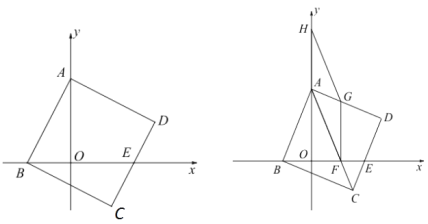
【题目】如图1,已知正方形ABCD的顶点A,B分别在y轴和x轴上,边CD交x轴的正半轴于点E.
(1)若A(0,a),且![]() ,求A点的坐标;
,求A点的坐标;
(2)在(l)的条件下,若3AO=4EO,求D点的坐标;
(3)如图2,连结AC交x轴于点F,点H是A点上方y轴上一动点,以AF、AH为边作平行四边形AFGH,使G点恰好落在AD边上,试探讨BF,HG与DG的数量关系,并证明你的结论.
参考答案:
【答案】(1)A(0,4)或(0,![]() );(2)D(4,2)或(4,
);(2)D(4,2)或(4,![]() );(3)2HG2+DG2=4BF2,详见解析
);(3)2HG2+DG2=4BF2,详见解析
【解析】
(1)由![]() ,得出a=±4,即可得出结果;
,得出a=±4,即可得出结果;
(2)当A(0,4)时,作DN⊥OE于N,作AM⊥DN于M,连AE,由AAS证得△AOB≌△AMD,得出AM=AO=4,求出EO=3,在Rt△AOE中,AE2=AO2+EO2=25,在Rt△ADE中,AD2+DE2=AE2,设D(4,m),代入求出m=2,即可得出结果;同理当A(0,-4)时,可求出D点坐标;
(3)作FP⊥AD于P,连DF,在Rt△AFP中,得到HG=AF=![]() PF,证明BF=DF与BF=GF,得出点P是DG的中点,在Rt△PDF中,PF2+DP2=DF2,即(
PF,证明BF=DF与BF=GF,得出点P是DG的中点,在Rt△PDF中,PF2+DP2=DF2,即(![]() )2+(
)2+(![]() )2=BF2,即可得出结果.
)2=BF2,即可得出结果.
(1)解:∵![]() ,
,
∴a=±4,
∴A点的坐标为(0,4)或(0,-4);
(2)当A点的坐标为(0,4)时
作DN⊥OE于N,作AM⊥DN于M,连AE,如图1所示:

则∠BAD=∠OAM=90°,
即∠BAO+∠OAD=∠OAD+∠DAM,
∴∠BAO=∠DAM,
∵四边形ABCD是正方形,
∴AB=AD,∠ADE=90°,
在△AOB与△AMD中,
 ,
,
∴△AOB≌△AMD(AAS),
∴AM=AO=4,
∴四边形AONM是正方形,
∴MN=ON=4,
∵3AO=4EO,
∴EO=3,
在Rt△AOE中,AE2=AO2+EO2=42+32=25,
在Rt△AMD中,AD2=AM2+DM2,
在Rt△DNE中,ED2=EN2+DN2,
在Rt△ADE中,AD2+DE2=AE2,
∴AM2+DM2+EN2+DN2=25,
设D(4,m),则DM=4m,EN=43=1,DN=m,
∴4span>2+(4m)2+12+m2=25,
∴m=2,
∴D(4,2)
当A点的坐标为(0,-4)时,
同理可得D(4,-2)
(3)解:2HG2+DG2=4BF2,理由如下:
过点F作FP⊥AD于P,连DF,如图2所示:

∵四边形AFGH是平行四边形,
∴HG=AF,AH∥GF,
∴∠FGA=∠GAH,
∴∠FGD=∠OAG,
∵四边形ABCD是正方形,
∴BC=DC,∠CAD=∠BCF=∠DCF=45°,∠BAD=∠CDA=∠ABC=90°,
∴△APF是等腰直角三角形,
∴PF=AP,
∴![]()
∴AF=![]() PF,
PF,
∴HG=AF=![]() PF,
PF,
故PF=![]() ,
,
在△BCF和△DCF中,
 ,
,
∴△BCF≌△DCF(SAS),
∴BF=DF,∠CBF=∠CDF,
∵∠FDG=90°∠CDF,∠ABO=90°∠CBF,
∴∠FDG=∠ABO,
∵∠OAG+∠OAB=90°,∠ABO+∠OAB=90°,
∴∠OAG=∠ABO,
∴∠FGD=∠FDG,
∴GF=DF=BF,
∴点P是DG的中点,
∴DP=![]() ,
,
在Rt△PDF中,PF2+DP2=DF2,
即(![]() )2+(
)2+(![]() )2=BF2,
)2=BF2,
∴2HG2+DG2=4BF2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)
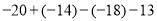 (2)
(2)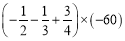
(3)﹣54×
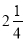 ÷
÷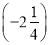 ×
×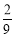 (4)
(4)
(5)﹣5×
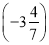 +(﹣9)×
+(﹣9)× +17×
+17×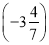 (6)
(6)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象上部分点的横坐标x与纵坐标y的对应值如下表所示:
x
…
-1
0
2
4
…
y
…
-5
1
1
m
…
求:(1)这个二次函数的解析式;
(2)这个二次函数图象的顶点坐标及上表中m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】农夫将苹果树种在正方形的果园内,为了保护苹果树不受风吹,他在苹果树的周围种上针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为( )
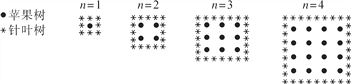
A. 6 B. 8 C. 12 D. 16
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线L上有三个正方形a,b,c,若a,c的面积分别为1和9,则b的面积为( )

A.8 B.9 C.10 D.11
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=4,射线BQ和AB互相垂直,点D是AB上的一个动点,点E在射线BQ上,BE=
 DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BQ于点C.设BE=x,BC=y,则y关于x的函数解析式为______________.
DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BQ于点C.设BE=x,BC=y,则y关于x的函数解析式为______________.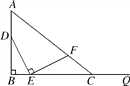
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠C=90°,BC=6,AC=8, P是斜边AB上一动点,PD⊥AC于点D,PE⊥BC于点E,则DE的长不可能是( )
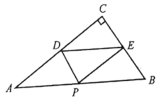
A.4B.5C.6D.7
相关试题

