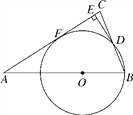
【题目】如图,在△ABC中,AB=AC,O在AB上,以O为圆心,OB长为半径的圆与BC交于点D,DE⊥AC于E.
(1)求证:DE是⊙O的切线;
(2)若AC与⊙O相切于F,AB=5,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接OD,由OB=OD,AB=AC,可得到∠ODB=∠C,即OD∥AC,而DE⊥AC,即可得到OD⊥DE,从而得到DE是⊙O的切线.
(2)根据切线的性质定理,连接过切点的半径,运用锐角三角函数的定义,用半径表示OA的长,再根据AB的长列方程求解.
(1)证明:连接OD,∵OB=OD,∴∠ABC=∠ODB.∵AB=AC,∴∠ABC=∠ACB,(2分)∴∠ODB=∠ACB,∴OD∥AC.∵DE⊥AC,∴OD⊥DE,∴DE是⊙O的切线.
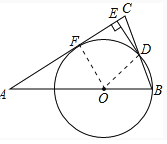
(2)解:连接OF,则OF⊥AC.∵在Rt△OAF中,sinA=![]() =
=![]() ,∴OA=
,∴OA=![]() OF.又∵AB=OA+OB=5,∴
OF.又∵AB=OA+OB=5,∴![]() OF+OF=5,∴OF=
OF+OF=5,∴OF=![]() ,∴⊙O的半径为
,∴⊙O的半径为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠C=90°,BC=6,AC=8, P是斜边AB上一动点,PD⊥AC于点D,PE⊥BC于点E,则DE的长不可能是( )
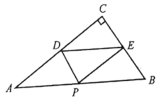
A.4B.5C.6D.7
-
科目: 来源: 题型:
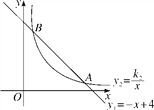
查看答案和解析>>【题目】如图,函数y1=-x+4的图象与函数y2=
 (x>0)的图象交于A(a,1)、B(1,b)两点.
(x>0)的图象交于A(a,1)、B(1,b)两点.(1)求函数y2的表达式;
(2)观察图象,比较当x>0时,y1与y2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):
第1批
第2批
第3批
第4批
第5批
3 km
10 km
-4 km
-3 km
-7 km
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)该驾驶员离公司距离最远是多少千米?
(3)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.
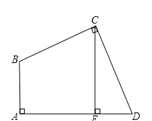
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题:
(1)求出足球和篮球的单价;
(2)若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案?
(3)在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知b是最小的正整数,且a、c满足|a+1|+(c+6)2=0.
(1)填空:a= ,b= ,c= ;
(2)a、b、c在数轴上所对应的点分别为A、B、C,P是数轴上点A、B之间一动点(不与点A、B重合),其对应的数为x,|x+1|+|x﹣1|= ;
(3)在(1)、(2)的条件下,点A、B、C开始在数轴上同时运动,若点C和点A分别以每秒6个单位长度和2个单位长度的速度向左运动,点B以每秒2个单位长度的速度向右运动,假设t秒钟过后,若点A与点C之间的距离表示为AC,点A与B之间的距离表示为AB.请问:AC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.

相关试题

