【题目】出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人,行驶路程记录如下(规定向南为正,向北为负,单位:km):
第1批 | 第2批 | 第3批 | 第4批 | 第5批 |
3 km | 10 km | -4 km | -3 km | -7 km |
(1)接送完第5批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)该驾驶员离公司距离最远是多少千米?
(3)若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?
参考答案:
【答案】(1)北;1千米 (2)13千米 (1)5.4升
【解析】
(1)计算出送完第5批客人后所处位置即可;
(2)分别计算出每次接送完一批客人后离公司距离即可求解;
(3)将各数的绝对值相加可得路程,再将路程乘以每千米耗油量.
解:(1)3+10-4-3-7=-1 km,
答:接送完第5批客人后,该驾驶员在公司北向,距离公司1千米,
故答案为:北;1千米;
(2)∵第一批离公司距离:3千米;
第二批:![]() =13千米;
=13千米;
第三批:![]() =9千米;
=9千米;
第四批:![]() =6千米;
=6千米;
第五批:![]() =1千米.
=1千米.
所以驾驶员离公司距离最远是13千米,
故答案为:13千米;
(3)(3 +10+4+3+7)×0.2=5.4(升).
答:共耗油5.4升.
故答案为:(1)北;1千米 (2)13千米 (1)5.4升.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB=4,射线BQ和AB互相垂直,点D是AB上的一个动点,点E在射线BQ上,BE=
 DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BQ于点C.设BE=x,BC=y,则y关于x的函数解析式为______________.
DB,作EF⊥DE,并截取EF=DE,连接AF并延长交射线BQ于点C.设BE=x,BC=y,则y关于x的函数解析式为______________.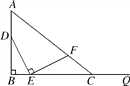
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在Rt△ABC中,∠C=90°,BC=6,AC=8, P是斜边AB上一动点,PD⊥AC于点D,PE⊥BC于点E,则DE的长不可能是( )
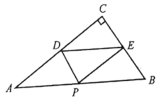
A.4B.5C.6D.7
-
科目: 来源: 题型:
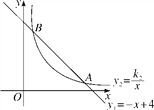
查看答案和解析>>【题目】如图,函数y1=-x+4的图象与函数y2=
 (x>0)的图象交于A(a,1)、B(1,b)两点.
(x>0)的图象交于A(a,1)、B(1,b)两点.(1)求函数y2的表达式;
(2)观察图象,比较当x>0时,y1与y2的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,O在AB上,以O为圆心,OB长为半径的圆与BC交于点D,DE⊥AC于E.
(1)求证:DE是⊙O的切线;
(2)若AC与⊙O相切于F,AB=5,sinA=
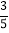 ,求⊙O的半径.
,求⊙O的半径.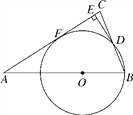
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.
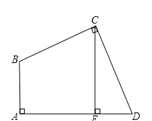
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题:
(1)求出足球和篮球的单价;
(2)若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案?
(3)在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多?
相关试题

