【题目】已知:如图,在四边形ABCD中,∠D=90°,∠ABC=∠BCD,点E在直线BC上,点F在直线CD上,且∠AEB=∠CEF.
(1)如图20①,若AE平分∠BAD,求证:EF⊥AE;
(2)如图20②,若AE平分四边形ABCD的外角,其余条件不变,则(1)中的结论是否仍然成立?并说明理由.

参考答案:
【答案】(1)见解析;(2) EF⊥AE仍成立,理由见解析.
【解析】
(1)如图1,先根据三角形内角和定理得出∠BAE=180°-∠B-∠AEB,∠EFC=180°-∠C-∠CEF,由∠B=∠C,∠AEB=∠CEF,得到∠BAE=∠EFC,再由角平分线定义得出∠BAE=∠DAE,等量代换得到∠EFC=∠DAE.由平角的定义得出∠EFC+∠EFD=180°,那么∠DAE+∠EFD=180°,再根据四边形内角和定理求出∠AEF+∠D=360°-(∠DAE+∠EFD)=180°,进而得到∠AEF=90°,由垂直的定义证明出EF⊥AE;
(2)如图2,先根据三角形外角的性质得出∠1=∠ABC-∠AEB,∠F=∠BCD-∠CEF,由∠ABC=∠BCD,∠AEB=∠CEF,得到∠1=∠F,再由角平分线定义得出∠1=∠2,等量代换得到∠F=∠2.由平角的定义得出∠2+∠EAD=180°,那么∠F+∠EAD=180°,再根据四边形内角和定理求出∠AEF+∠D=360°-(∠F+∠EAD)=180°,进而得到∠AEF=90°,由垂直的定义得出EF⊥AE.
(1)证明:如图1,∵∠BAE=180°-∠B-∠AEB,∠EFC=180°-∠C-∠CEF,
∠B=∠C,∠AEB=∠CEF,
∴∠BAE=∠EFC,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠EFC=∠DAE.
∵∠EFC+∠EFD=180°,
∴∠DAE+∠EFD=180°,
∴∠AEF+∠D=360°-(∠DAE+∠EFD)=180°,
∵∠D=90°,
∴∠AEF=90°,
∴EF⊥AE;
(2)解:如图2,若AE平分∠BAD的外角,其余条件不变,(1)中结论没有变化.理由如下:
∵∠1=∠ABC-∠AEB,∠F=∠BCD-∠CEF,
∠ABC=∠BCD,∠AEB=∠CEF,
∴∠1=∠F,
∵AE平分∠BAD的外角,
∴∠1=∠2,
∴∠F=∠2.
∵∠2+∠EAD=180°,
∴∠F+∠EAD=180°,
∴∠AEF+∠D=360°-(∠F+∠EAD)=180°,
∵∠D=90°,
∴∠AEF=90°,
∴EF⊥AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ACB和△DCE均为等边三角形,若B,D,E在同一直线上,连接AE.

(1)请你在图中找出一个与△AEC全等的三角形:;
(2)∠AEB的度数为;CE,AE,BE的数量关系为 .
(3)如图2,△ACB是等腰直角三角形,∠AEB=90°,连接CE,过点C作CD⊥CE,交BE于点D,试探究CE,AE,BE的数量关系,并说明理由.
(4)如图3,在正方形ABCD中,CD=5 ,点P为正方形ABCD外一点,∠APC=90°,且AP=6,试求点P到CD的距离.
,点P为正方形ABCD外一点,∠APC=90°,且AP=6,试求点P到CD的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)为了吸引顾客,某商家把每件100元进的一批服装,标价定为每件498元,然后以标价的5折出售,则售价为_______元,利润为_______元,利润率为_______(填百分数);
(2)请结合下面方程的数据在空白处填上一个合适的条件,使问题成为一个完整的打折销售的实际问题并求解.
某商家将一件成本为200元的衣服_______标价,再按标价的x折出售,仍可获利40元,求x.
200×(1+50%)
 -200=40.
-200=40. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2等于度.

-
科目: 来源: 题型:
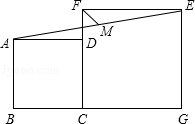
查看答案和解析>>【题目】如图,正方形ABCD和正方形CGEF的边长分别是3和5,且点B、C、G在同一直线上,M是线段AE的中点,连接MF,则MF的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)计算:(﹣ )﹣2+2cos30°﹣|﹣
)﹣2+2cos30°﹣|﹣  |﹣(π﹣2017)0
|﹣(π﹣2017)0
(2)化简:( ﹣x+1)÷
﹣x+1)÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】小王玩游戏:一张纸片,第一次将其撕成四小片,以后每次都将其中一片撕成更小的四片,如此进行下去.

(1)填空:当小王撕了3次后,共有________张纸片;
(2)填空:当小王撕了n次后,共有________张纸片.(用含n的代数式表示)
(3)小王说:我撕了若干次后,共有纸片2013张,小王说的对不对?若不对,请说明你的理由;若对的,请指出小王需撕多少次?
相关试题

