【题目】小王玩游戏:一张纸片,第一次将其撕成四小片,以后每次都将其中一片撕成更小的四片,如此进行下去.

(1)填空:当小王撕了3次后,共有________张纸片;
(2)填空:当小王撕了n次后,共有________张纸片.(用含n的代数式表示)
(3)小王说:我撕了若干次后,共有纸片2013张,小王说的对不对?若不对,请说明你的理由;若对的,请指出小王需撕多少次?
参考答案:
【答案】(1)10;(2)(3n+1);(3)不对,理由见解析.
【解析】
试题从提议可知,每撕一次,纸片就增加3张,即撕第一次,有(1+3)张,第二次有(1+3×2)张,第三次有(1+3×3)张……所以撕了n次后有(3n+1)张;小王撕了若干次后,共有纸片2013张,即3n+1=2013,解得n=670![]() ,由于撕的次数只能为整数,所以小王说的不对.
,由于撕的次数只能为整数,所以小王说的不对.
试题解析:(1)10.
(3n+1).
(3)解:由题意得
3n+1=2013 解得n=670![]() .
.
因为n不是正整数,所以小王说的不对.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,∠D=90°,∠ABC=∠BCD,点E在直线BC上,点F在直线CD上,且∠AEB=∠CEF.
(1)如图20①,若AE平分∠BAD,求证:EF⊥AE;
(2)如图20②,若AE平分四边形ABCD的外角,其余条件不变,则(1)中的结论是否仍然成立?并说明理由.

-
科目: 来源: 题型:
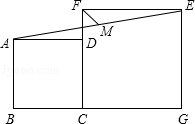
查看答案和解析>>【题目】如图,正方形ABCD和正方形CGEF的边长分别是3和5,且点B、C、G在同一直线上,M是线段AE的中点,连接MF,则MF的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)计算:(﹣ )﹣2+2cos30°﹣|﹣
)﹣2+2cos30°﹣|﹣  |﹣(π﹣2017)0
|﹣(π﹣2017)0
(2)化简:( ﹣x+1)÷
﹣x+1)÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.

(1)填空:与∠AOE互补的角是 ;
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某机器零件的横截面如图所示,按要求线段AB和DC的延长线相交成直角才算合格,一工人测得∠A=23°,∠D=31°,∠AED=143°,请你帮他判断该零件是否合格:___.(填“合格”或“不合格”)

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读思考
我们知道,在数轴上|a|表示数a所对应的点到原点的距离,这是绝对值的几何意义,由此我们可进一步地来研究数轴上任意两个点之间的距离,一般地,如果数轴上两点A、B 对立的数用a,b表示,那么这两个点之间的距离AB=|a﹣b|.也可以用两点中右边的点所表示数的减去左边的点所表示的数来计算,例如:数轴上P,Q两点表示的数分别是﹣1和2,那么P,Q两点之间的距离就是 PQ=2﹣(﹣1)=3.
启发应用
如图,点A在数轴上对应的数为a,点B对应的数为b,且a、b满足|a+3|+(b﹣2)2=0
(1)求线段AB的长;
(2)如图,点C在数轴上对应的数为x,且x是方程2x+1=
 x﹣8的解,
x﹣8的解,①求线段BC的长;
②在数轴上是否存在点P使PA+PB=BC?若存在,直接写出点P对应的数:若不存在,说明理由.
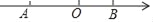
相关试题

