【题目】如图1,△ACB和△DCE均为等边三角形,若B,D,E在同一直线上,连接AE.
(1)请你在图中找出一个与△AEC全等的三角形:;
(2)∠AEB的度数为;CE,AE,BE的数量关系为 .
(3)如图2,△ACB是等腰直角三角形,∠AEB=90°,连接CE,过点C作CD⊥CE,交BE于点D,试探究CE,AE,BE的数量关系,并说明理由.
(4)如图3,在正方形ABCD中,CD=5 ![]() ,点P为正方形ABCD外一点,∠APC=90°,且AP=6,试求点P到CD的距离.
,点P为正方形ABCD外一点,∠APC=90°,且AP=6,试求点P到CD的距离.
参考答案:
【答案】
(1)△BDC
(2)60°;CE+AE=BE
(3)
解:∵CD⊥CE,∠ACB=90°,
∴∠ECA=∠DCB,
∵∠AEB=90°,∠ACB=90°,
∴A、E、C、B四点共圆,
∴∠EAC=∠DBC,
在△AEC和△BDC中,
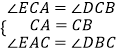 ,
,
∴△AEC≌△BDC,
∴AE=BD,CE=CD,
∴△ECD是等腰直角三角形,
∴ED= ![]() CE,
CE,
∴BE=DE+BD= ![]() CE+AE
CE+AE
(4)
解:当点P在AD上方时,连接AC、PD,作PH⊥CD交AD的延长线于H,
∵AD=5 ![]() ,
,
∴AC=10,
则PC= ![]() =8,
=8,
由拓展探究可知,PD= ![]() =
= ![]() ,
,
∵PH∥AD,
∴∠DPH=∠ADP,
∴∠DPH=∠ACP,
∴PH=PD× ![]() =
= ![]() ;
;
当点P在AB的左侧时,同理PH= ![]() .
.
【解析】解:(1)△AEC≌△BDC,
证明:∵△ACB和△DCE均为等边三角形,
∴∠ECD=∠ACB=60°,
∴∠ECA=∠DCB,
在△AEC和△BDC中,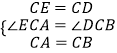 ,
,
∴△AEC≌△BDC,
所以答案是:△BDC;
⑵∠CDB=180°﹣∠CDE=120°,
∵△AEC≌△BDC,
∴∠AEC=∠CDB=120°,AE=BD,
∴∠AEB=60°,
BE=DE+BD=CE+AE;
所以答案是:60°;CE+AE=BE;
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)﹣0.5﹣(﹣3
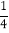 )+2.75﹣(+7
)+2.75﹣(+7 )
)(2)(
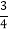 +
+ ﹣
﹣ )×(﹣12)
)×(﹣12)(3)(﹣2)3÷
 ×
×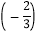 2
2(4)﹣12﹣
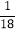 ×[2﹣(﹣4)2]
×[2﹣(﹣4)2] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,学校有一个长方形广场,在广场的中央设计一个圆形花坛,四角都设计四分之一圆形的花坛.若长方形的长为am,宽为bm,中央圆形的半径和四个四分之一圆形的半径都为rm.
(1)列式表示广场空地的面积;(不写过程,直接写出答案)
(2)学校准备在广场四周种树,七年级四个班的学生在植树节当天进行义务植树,一班植树 x棵,二班植树的棵数比一班的多10棵,三班植树的棵数比二班的2倍少30棵,四班植树的棵数比三班的一半多20棵,求四个班一共植树多少棵?(用含x的式子表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线C1:y1=tx2﹣1(t>0)和抛物线C2:y2=﹣4(x﹣h)2+1(h≥1).
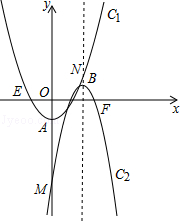
(1)两抛物线的顶点A、B的坐标分别为和;
(2)设抛物线C2的对称轴与抛物线C1交于点N,则t为何值时,A、B、M、N为顶点的四边形是平行四边形.
(3)设抛物线C1与x轴的左交点为点E,抛物线C2与x轴的右边交点为点F,试问,在第(2)问的前提下,四边形AEBF能否为矩形?若能,求出h值;若不能,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题
(1)为了吸引顾客,某商家把每件100元进的一批服装,标价定为每件498元,然后以标价的5折出售,则售价为_______元,利润为_______元,利润率为_______(填百分数);
(2)请结合下面方程的数据在空白处填上一个合适的条件,使问题成为一个完整的打折销售的实际问题并求解.
某商家将一件成本为200元的衣服_______标价,再按标价的x折出售,仍可获利40元,求x.
200×(1+50%)
 -200=40.
-200=40. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线m∥n,△ABC的顶点B,C分别在直线n,m上,且∠ACB=90°,若∠1=40°,则∠2等于度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,∠D=90°,∠ABC=∠BCD,点E在直线BC上,点F在直线CD上,且∠AEB=∠CEF.
(1)如图20①,若AE平分∠BAD,求证:EF⊥AE;
(2)如图20②,若AE平分四边形ABCD的外角,其余条件不变,则(1)中的结论是否仍然成立?并说明理由.

相关试题

