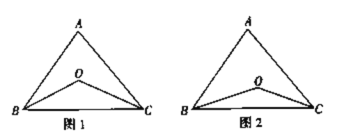
【题目】已知任意一个三角形的三个内角的和是180°,如图1,在ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.
(1)若∠A=70°,求∠BOC的度数;
(2)若∠A=α,求∠BOC的度数;
(3)如图2,若BO、CO分别是∠ABC、∠ACB的三等分线,也就是∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A=α,求∠BOC的度数.
∠ACB,∠A=α,求∠BOC的度数.
参考答案:
【答案】(1)125°;(2)90°+![]() ;(3)120°+
;(3)120°+![]()
【解析】
(1)根据三角形的内角和定理求出∠ABC+∠ACB,根据角平分线的定义求出∠OBC+∠OCB,根据三角形内角和定理求出即可;
(2)根据三角形的内角和定理求出∠ABC+∠ACB,根据角平分线的定义求出∠OBC+∠OCB,根据三角形内角和定理求出即可;
(3)根据三角形的内角和定理求出∠ABC+∠ACB,求出∠OBC+∠OCB,根据三角形内角和定理求出即可.
(1)∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=110°,
∵在△ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=55°,
(∠ABC+∠ACB)=55°,
∴∠BOC=180°-(∠OBC+∠OCB)=125°;
(2)∵∠A=α,
∴∠ABC+∠ACB=180°-∠A=180°-α,
∵在△ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-α)=90°-
(180°-α)=90°-![]() α,
α,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-![]() α)=90°+
α)=90°+![]() α;
α;
(3)∵∠A=α,
∴∠ABC+∠ACB=180°-∠A=180°-α,
∵∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC+∠OCB=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)=![]() (180°-α)=60°-
(180°-α)=60°-![]() α,
α,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(60°-![]() α)=120°+
α)=120°+![]() α.
α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,BC=2
 .点P从点A出发沿沿射线AB以1
.点P从点A出发沿沿射线AB以1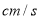 的速度运动,过点P作PE∥BC交射线AC于点E,同时点Q从点C出发沿BC的延长线以1
的速度运动,过点P作PE∥BC交射线AC于点E,同时点Q从点C出发沿BC的延长线以1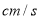 的速度运动,连结BE、EQ.设点P的运动时间为t(
的速度运动,连结BE、EQ.设点P的运动时间为t( ).
). 
(1)求证:△APE是等边三角形;
(2)直接写出CE的长(用含
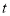 的代数式表示);
的代数式表示);(3)当点P在边AB上,且不与点A、B重合时,求证:△BPE≌△ECQ.
(4)在不添加字母和连结其它线段的条件下,当图中等腰三角形的个数大于3时,直接写出t的值和对应的等腰三角形的个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形第四个顶点坐标的是( )

A. (3,-1) B. (-1,-1) C. (1,1) D. (-2,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC=a.作BC边的三等分点C1,使得CC1:BC1=1:2,过点C1作AC的平行线交AB于点A1,过点A1作BC的平行线交AC于点D1,作BC1边的三等分点C2,使得C1C2:BC2=1:2,过点C2作AC的平行线交AB于点A2,过点A2作BC的平行线交A1C1于点D2;如此进行下去,则线段AnDn的长度为______________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人分别在六次射击中的成绩如下表:(单位:环)
第1次
第2次
第3次
第4次
第5次
第6次
甲
6
7
7
8
6
8
乙
5
9
6
8
5
9
分别算出两人射击的平均数和方差.这六次射击中成绩发挥比较稳定的是谁?
-
科目: 来源: 题型:
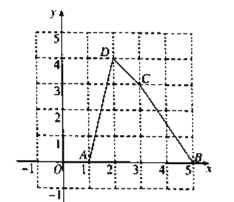
查看答案和解析>>【题目】如图所示,在平面直角坐标系中有四边形ABCD.
(1)写出四边形ABCD的顶点坐标;
(2)求线段AB的长;
(3)求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC.
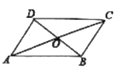
(1)求证:四边形ABCD是平行四边形
(2)若AC⊥BD,且AB=4,则四边形ABCD的周长为________.
相关试题

