【题目】如图,AC⊥BD 于点 , 是 AB 上一点,FD 交 AC 于点 E,∠B 与 ∠D 互余.

(1)试说明:∠A=∠D;
(2)若 AE=1,AC=CD=2.5,求 BD 的长.
参考答案:
【答案】(1)见解析;(2)4.
【解析】(1)只要证明∠A+∠B=90°,∠D+∠B=90°即可解决问题;
(2)只要证明△ACB≌△DCF(ASA),即可推出BC=CE=1.5,由此即可解决问题;
详(1)证明:∵AC⊥BD,
∴∠A+∠B=90°,∠ACB=90°=∠DCE,
∵∠B+∠D=90°,
∴∠A=∠D.
(2)∵AE=1,AC=2.5,
∴EC=AC-AE=1.5,
∵∠B+∠D=90°,
∴∠BFD=90°,
∵∠ACB=90°,
∴∠BFD=∠ACD,
在△ACB和△DCF中,
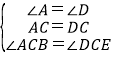 ,
,
∴△ACB≌△DCF(ASA),
∴BC=CE=1.5,
∴BD=BC+CD=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在 △ABC 中,∠C=90°,DB⊥BC 于点 ,分别以点 D 和点 为圆心,以大于
 的长为半径作弧,两弧相交于点 E 和点 ,作直线 EF,延长 AB 于点 ,连接 DG,下面是说明 ∠A=∠D 的说理过程,请把下面的说理过程补充完整:
的长为半径作弧,两弧相交于点 E 和点 ,作直线 EF,延长 AB 于点 ,连接 DG,下面是说明 ∠A=∠D 的说理过程,请把下面的说理过程补充完整:因为 DB⊥BC(已知),
所以 ∠DBC=90°( ) .
因为 ∠C=90°(已知),
所以 ∠DBC=∠C(等量代换),
所以 DB∥AC ( ) ,
所以 (两直线平行,同位角相等);
由作图法可知:直线 EF 是线段 DB 的 ( ) ,
所以 GD=GB,线段 (上的点到线段两端点的距离相等),
所以 ( ) ,因为 ∠A=∠1(已知),
所以 ∠A=∠D(等量代换).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.
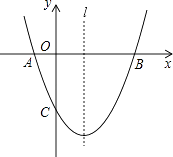
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
A.
B.
C.
D.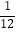
-
科目: 来源: 题型:
查看答案和解析>>【题目】若t为实数,关于x的方程x2﹣4x+t﹣2=0的两个非负实数根为a、b,则代数式(a2﹣1)(b2﹣1)的最小值是( )
A.﹣15
B.﹣16
C.15
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,AC为对角线,点E为AC上一点,连接EB,ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,当∠BED=120°时,求∠EFD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,E 是直线 CD 上的一点,且 ∠BAE=30°, 是直线 CD 上的一动点,M是 AP 的中点,直线 MN⊥AP 且与 CD 交于点 N,设 ∠BAP=X°,∠MNE=Y°.

(1)在图2 中,当 x=12 时,∠MNE= ;在图 3 中,当 x=50 时,∠MNE= ;

(2)研究表明:y与x之间关系的图象如图4所示( 不存在时,用空心点表示),请你根据图象直接估计当 y=100 时,x= ;

(3)探究:当 x= 时,点 N 与点 E 重合;
(4)探究:当 x>105 时,求y与x之间的关系式.
相关试题

