【题目】如图,![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.

(1)求![]() 的面积;
的面积;
(2)如果要使![]() 与
与![]() 全等,那么点
全等,那么点![]() 的坐标是多少?
的坐标是多少?
(3)求![]() 的边
的边![]() 上的高.
上的高.
参考答案:
【答案】(1)3;(2)(4,-1)或(-1,3)或(-1,-1);(3)![]() .
.
【解析】
(1)观察可得点B的坐标为(3,1),利用三角形的面积公式即可求解;
(2)因为△ABD与△ABC有一条公共边AB,故应从点D在AB的上边、点D在AB的下边两种情况入手进行讨论,即可得出答案;
(3)先根据勾股定理求出AC,设![]() 的边
的边![]() 上的高是h,根据三角形的面积公式即可求解.
上的高是h,根据三角形的面积公式即可求解.
解:(1)观察可得点B的坐标为(3,1),则AB=3,
∴![]() =3;
=3;
(2)△ABD与△ABC有一条公共边AB,
当点D在AB的下边时,点D有两种情况:①坐标是(4,-1);②坐标为(-1,-1);
当点D在AB的上边时,坐标为(-1,3);
点D的坐标是(4,-1)或(-1,3)或(-1,-1);
(3)设![]() 的边
的边![]() 上的高是h,
上的高是h,
AC=![]() ,
,
![]() ,即
,即![]() ,
,
解得:h=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:p为实数.
p
k
q
…
…
…
3
16×3+26
2×2×6
4
16×4+26
2×3×7
5
16×5+26
2×4×8
6
16×6+26
2×5×9
7
16×7+26
2×6×10
…
…
…
根据上表中的规律,回答下列问题:
(1)当p为何值时,k=38?
(2)当p为何值时,k与q的值相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学老师在一次“探究性学习”课中,设计了如下数表:

2
3
4
5
…

3
8
15
24
…

4
6
8
10
…

5
10
17
26
…
由表可知,当
 时,
时, ,
, ,
, ;
;当
 时,
时, ,
, ,
, ;
;………
(1)当
 时,
时, ________,
________, _________,
_________, ________.
________. (2)请你分别观察
 ,
, ,
, 与
与 之间的关系,并分别用含有
之间的关系,并分别用含有 的代数式表示
的代数式表示  ,
, ,
, .
.  ________,
________, _________,
_________, ________.
________. (3)猜想以
 ,
, ,
, 为边的三角形是否为直角三角形,并说明理由.
为边的三角形是否为直角三角形,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣6x﹣k2=0(k为常数).
(1)求证:方程有两个不相等的实数根;
(2)设x1,x2为方程的两个实数根,且x1+2x2=14,试求出方程的两个实数根和k的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示的是嘉淇爸爸给嘉淇出的一道题,如图2所示的是嘉淇对该题的解答.她所写的结论中,正确的个数是( )
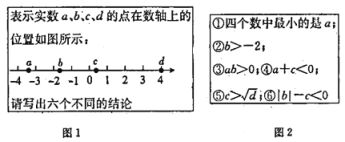
A.6B.5C.4D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,AC=2,BC=4,CD=BD=DE,则CE=( )
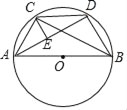
A. 3﹣
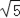 B.
B. 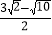 C.
C. 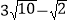 D.
D. 
相关试题

