【题目】数学老师在一次“探究性学习”课中,设计了如下数表:
| 2 | 3 | 4 | 5 | … |
| 3 | 8 | 15 | 24 | … |
| 4 | 6 | 8 | 10 | … |
| 5 | 10 | 17 | 26 | … |
由表可知,当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,
,![]() ;
;
………
(1)当![]() 时,
时,![]() ________,
________,![]() _________,
_________,![]() ________.
________.
(2)请你分别观察![]() ,
,![]() ,
,![]() 与
与![]() 之间的关系,并分别用含有
之间的关系,并分别用含有![]() 的代数式表示
的代数式表示 ![]() ,
,![]() ,
,![]() .
.
![]() ________,
________,![]() _________,
_________,![]() ________.
________.
(3)猜想以![]() ,
,![]() ,
,![]() 为边的三角形是否为直角三角形,并说明理由.
为边的三角形是否为直角三角形,并说明理由.
参考答案:
【答案】(1)35,12,37;(2)![]() -1, 2n,
-1, 2n, ![]() +1;(3)是直角三角形,理由见解析.
+1;(3)是直角三角形,理由见解析.
【解析】
(1)观察表中的数据,可以发现a,b,c与n的关系,a与c正好是n2加减1,b=2n,即可得出答案;
(2)观察表中的数据即可得![]() ,
,![]() ,
,![]() 与
与![]() 之间的关系;
之间的关系;
(3)利用完全平方公式计算出a2+b2的值,以及c2的值,再利用勾股定理逆定理即可求出.
解:(1)由表格中的数据得到:a=![]() -1,b=2n,c=
-1,b=2n,c=![]() +1,
+1,
∴当![]() 时,
时,![]() 35,
35,![]() 12,
12, ![]() 37;
37;
(2)观察表中的数据得到:a与c正好是n2加减1,b=2n,
∴![]() ,
,![]() ,
,![]() 与
与![]() 之间的关系,分别用含有
之间的关系,分别用含有![]() 的代数式表示为:
的代数式表示为:
![]()
![]() -1,
-1,![]() 2n,
2n,![]()
![]() +1;
+1;
(3)猜想:以![]() ,
,![]() ,
,![]() 为边的三角形是直角三角形,
为边的三角形是直角三角形,
理由:∵![]() ,
,
![]() ,
,
∴![]() ,
,
∴以![]() ,
,![]() ,
,![]() 为边的三角形是直角三角形.
为边的三角形是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,∠ABC=60°,CD平分∠ACB交AB于点D,点E在线段CD上(点E不与点C. D重合),且∠EAC=2∠EBC.

(1)如图1,若∠EBC=27°,且EB=EC,则∠DEB=___°,∠AEC=___°.
(2)如图2,①求证:AE+AC=BC;
②若∠ECB=30°,且AC=BE,求∠EBC的度数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,小正方形方格的边长为 1,
按要求作图,并根据要求解答问题:

(1)作图:连接图中小正方形方格的某两个顶点,分别得到三条线段
 、
、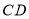 、
、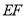 ,使得
,使得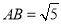 、
、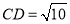 、
、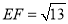 ;
;(2)判断(1)中的三条线段
 、
、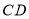 、
、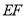 能否构成三角形,并说明理由.
能否构成三角形,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:p为实数.
p
k
q
…
…
…
3
16×3+26
2×2×6
4
16×4+26
2×3×7
5
16×5+26
2×4×8
6
16×6+26
2×5×9
7
16×7+26
2×6×10
…
…
…
根据上表中的规律,回答下列问题:
(1)当p为何值时,k=38?
(2)当p为何值时,k与q的值相等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣6x﹣k2=0(k为常数).
(1)求证:方程有两个不相等的实数根;
(2)设x1,x2为方程的两个实数根,且x1+2x2=14,试求出方程的两个实数根和k的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,点
中,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 .
. 
(1)求
 的面积;
的面积;(2)如果要使
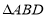 与
与 全等,那么点
全等,那么点 的坐标是多少?
的坐标是多少?(3)求
 的边
的边 上的高.
上的高. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示的是嘉淇爸爸给嘉淇出的一道题,如图2所示的是嘉淇对该题的解答.她所写的结论中,正确的个数是( )
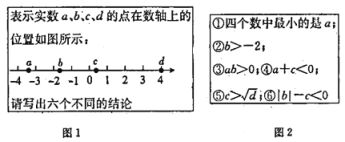
A.6B.5C.4D.3
相关试题

