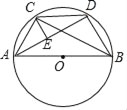
【题目】如图,AB为⊙O的直径,AC=2,BC=4,CD=BD=DE,则CE=( )
A. 3﹣![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】D
【解析】
先根据勾股定理计算直径AB=![]() =2
=2![]() ,作垂线DP和DQ,根据角平分线的性质得:DP=DQ,由全等可得AP=AQ,设未知数列等式,可得PC和BQ的长,再根据等腰三角形的性质得:∠DEC=∠DCE,根据外角性质得:∠ACE=∠ECB,则∠ACE=∠ECB=45°,作辅助线后可得:△EFC是等腰直角三角形,设EF=FC=a,则CE=
,作垂线DP和DQ,根据角平分线的性质得:DP=DQ,由全等可得AP=AQ,设未知数列等式,可得PC和BQ的长,再根据等腰三角形的性质得:∠DEC=∠DCE,根据外角性质得:∠ACE=∠ECB,则∠ACE=∠ECB=45°,作辅助线后可得:△EFC是等腰直角三角形,设EF=FC=a,则CE=![]() a,AF=2-a,根据△AFE∽△APD,列比例式可得a的值,求CE的长.
a,AF=2-a,根据△AFE∽△APD,列比例式可得a的值,求CE的长.
∵AB是⊙O的直径,
∴∠ACB=90°,
∵AC=2,BC=4,
∴AB=![]() =2
=2![]() ,
,
∵CD=BD,
∴![]() ,
,
∴∠CAD=∠BAD,
过D作DP⊥AC于P,DQ⊥AB于Q,连接OD,
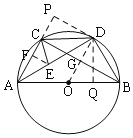
∴PD=DQ,
∴Rt△DPC≌Rt△DQB(HL),
∴CP=BQ,
易得△APD≌△AQD,
∴AP=AQ,
设PC=x,则AP=2+x,AQ=AB-BQ=2![]() -x,
-x,
∴2+x=2![]() -x,
-x,
x=![]() -1,
-1,
∴BQ=CP=![]() -1,OQ=1,
-1,OQ=1,
Rt△ODQ中,DQ=PD=![]() =2,
=2,
∵DE=DC,
∴∠DEC=∠DCE,
∵∠DEC=∠CAD+∠ACE,∠DCE=∠ECB+∠ACE,
∴∠CAD+∠ACE=∠ECB+∠DCB,
∵![]() ,
,
∴∠CAD=∠DCB,
∴∠ACE=∠ECB,
∵∠ACB=90°,
∴∠ACE=∠ECB=45°,
过E作EF⊥AP于F,
∴△EFC是等腰直角三角形,
设EF=FC=a,则CE=![]() a,AF=2-a,
a,AF=2-a,
∵EF∥PD,
∴△AFE∽△APD,
∴![]() ,
,
∴![]() ,
,
∴a=3-![]() ,
,
∴CE=![]() a=
a=![]() (3-
(3-![]() )=3
)=3![]() -
-![]() .
.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,点
中,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 .
. 
(1)求
 的面积;
的面积;(2)如果要使
 与
与 全等,那么点
全等,那么点 的坐标是多少?
的坐标是多少?(3)求
 的边
的边 上的高.
上的高. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示的是嘉淇爸爸给嘉淇出的一道题,如图2所示的是嘉淇对该题的解答.她所写的结论中,正确的个数是( )
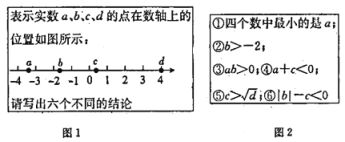
A.6B.5C.4D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC看,∠BAC=90°,AC=12,AB=10,D是AC上一个动点,以AD为直径的⊙O交BD于E,则线段CE的最小值是( )

A. 5 B. 6 C. 7 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=4,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连结EF,则线段EF长度的最小值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我国南宋著名数学家秦九韶的著作《数书九章》里记载着这样一道题:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”这道题的大意是:有一块三角形沙田,三条边长分别为5里;12里;13里,问这块沙田面积有多大?题中的1里=0.5千米,则该沙田的面积为( )
A.3平方千米B.7.5平方千米C.15平方千米D.30平方千米
相关试题

