【题目】如图,将一个三角板放在边长为1的正方形![]() 上,并使它的直角顶点
上,并使它的直角顶点![]() 在对角线
在对角线![]() 上滑动,直角的一边始终经过点
上滑动,直角的一边始终经过点![]() ,另一边与射线
,另一边与射线![]() 相交于点
相交于点![]() .
.

(1)当点![]() 在
在![]() 边上时,过点
边上时,过点![]() 作
作![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,证明:
,证明:![]() ;
;
(2)当点![]() 在线段
在线段![]() 的延长线上时,设
的延长线上时,设![]() 、
、![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 的长为
的长为![]() .
.
①直接写出![]() 与
与![]() 之间的函数关系,并写出函数自变量
之间的函数关系,并写出函数自变量![]() 的取值范围;
的取值范围;
②![]() 能否为等腰三角形?如果能,直接写出相应的
能否为等腰三角形?如果能,直接写出相应的![]() 值;如果不能,说明理由.
值;如果不能,说明理由.
参考答案:
【答案】(1)见解析;(2)① .②
.②![]() 能为等腰三角形,
能为等腰三角形,![]() .
.
【解析】
(1)根据正方形的性质证明![]() ,即可求解;
,即可求解;
(2)①根据题意作图,由正方形的性质可知当![]() 时,点
时,点![]() 在线段
在线段![]() 的延长线上,同理可得
的延长线上,同理可得![]() ,得到MP=NQ,利用等腰直角三角形的性质可知MP=
,得到MP=NQ,利用等腰直角三角形的性质可知MP=![]() x,NC=CD-DN=1-
x,NC=CD-DN=1-![]() x,CQ=y,代入MP=NQ化简即可求解;
x,CQ=y,代入MP=NQ化简即可求解;
②由![]() 是等腰三角形,∠PCQ=135°,CP=CQ成立,代入解方程即可求解 ,
是等腰三角形,∠PCQ=135°,CP=CQ成立,代入解方程即可求解 ,
(1)证明:∵在正方形![]() 中,
中,![]() 为对角线,
为对角线,
∴![]() ,
,![]() ,∵
,∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,
∵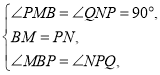
∴![]() ,∴
,∴![]() .
.
(2)①如图,点![]() 在线段
在线段![]() 的延长线上,
的延长线上,
同(1)可证![]() ,
,
∴MP=NQ,
在等腰直角三角形AMP中,AP=![]() =x
=x
∴MP=![]() x=AM,
x=AM,
∴NC=BM=AB-AM=1-![]() x
x
故NQ=NC+CQ=1-![]() x+y
x+y
∴![]() x=1-
x=1-![]() x+y
x+y
化简得![]()
当P点位于AC中点时,Q点恰好在C点,又AP<AC=![]()
∴![]()
∴![]() 与
与![]() 之间的函数关系是
之间的函数关系是![]() (
(![]() )
)
②当![]() 时,
时,![]() 能为等腰三角形,
能为等腰三角形,
理由:当点![]() 在
在![]() 的延长线上,CQ=
的延长线上,CQ=![]() ,CQ=AC-AP=
,CQ=AC-AP=![]() ,
,
由![]() 是等腰三角形,∠PCQ=∠PCB+∠BCQ=45°+90°=135°,
是等腰三角形,∠PCQ=∠PCB+∠BCQ=45°+90°=135°,
∴CP=CQ成立,
即![]() 时,解得
时,解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校七年级举行“每天锻炼一小时,健康生活一辈子”为主题的一分钟跳绳大赛,校团委组织了全级1000名学生参加为了解本次大赛的成绩,校团委随机抽取了其中100名学生的成绩(成绩取整数,总分100分)作为样本进行统计,制成如下不完整的统计图表根据所给信息,解答下列问题:
(1)m=______,n=_____.
(2)补全频数分布直方图;
(3)若成绩在80分以上(包括80分)为“优”,请你估计该校七年级参加本次比赛的1000名学生中成绩是“优”的有多少人

-
科目: 来源: 题型:
查看答案和解析>>【题目】把二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y=
 (x+1)2-1的图象.
(x+1)2-1的图象.(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向,对称轴和顶点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为引导学生“爱读书,多读书,读好书”,某校七(2)班决定购买A、B两种书籍.若购买A种书籍1本和B种书籍3本,共需要180元;若购买A种书籍3本和B种书籍1本,共需要140元.
(1)求A、B两种书籍每本各需多少元?
(2)该班根据实际情况,要求购买A、B两种书籍总费用不超过700元,并且购买B种书籍的数量是A种书籍的
 ,求该班本次购买A、B两种书籍有哪几种方案?
,求该班本次购买A、B两种书籍有哪几种方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线
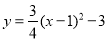 .
.(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
 的图象与
的图象与 轴交于点
轴交于点 ,与
,与 轴交于点
轴交于点 ,过
,过 的中点
的中点 的直线
的直线 交
交 轴于点
轴于点 .
.
(1)求
 ,
, 两点的坐标及直线
两点的坐标及直线 的函数表达式;
的函数表达式;(2)若坐标平面内的点
 ,能使以点
,能使以点 ,
, ,
, ,
, 为顶点的四边形为平行四边形,请直接写出满足条件的点
为顶点的四边形为平行四边形,请直接写出满足条件的点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)直接写出点C的坐标.
(2)在y轴上是否存在点P,使得S△POB=
 S△ABC若存在,求出点P的坐标;若不存在,请说明理由.
S△ABC若存在,求出点P的坐标;若不存在,请说明理由.(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.

相关试题

